Question 1167492: A polynomial P(x) has all real coefficients and z is a complex number.
If P(x)P(x') = 16, Find |P(x)|, giving reasons.
Note that x' is the conjugate of x and the answer should be 4.
I have no idea where to start with this question
Answer by ikleyn(52771)   (Show Source):
You can put this solution on YOUR website! .
A polynomial P(x) has all real coefficients and z is a complex number.
If P(x)P(x') = 16, Find |P(x)|, giving reasons.
Note that x' is the conjugate of x and the answer should be 4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since the polynomial P(x) has real coefficients, we can write
(P(x))' = P(x').
In other words, the conjugate to P(x), i.e. (P(x))', is equal to P(x').
It is a consequence of basic properties of complex numbers.
So, we can write for |P(x)|
16 = P(x)*P(x') = P(x)*(P(x))' = |P(x)|^2.
Thus we learned that |P(x)^2 = 16.
It implies |P(x)| = 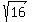 = 4.
At this point, the problem is just solved completely.
ANSWER. At given conditions, |P(x)| = 4.
Solved in full with complete explanations.
It is good educative problem on complex numbers.
If you have basic knowledge on Complex numbers, then this explanation should be enough to you.
If, on contrary, it is not enough to you, it means that you have no necessary basic knowledge on Complex numbers.
|
|
|
