Question 1140623: find the square roots of 1+6i
Found 2 solutions by dkppathak, ikleyn:
Answer by dkppathak(439)   (Show Source):
You can put this solution on YOUR website! find the square roots of 1+6i
solution
let x+iy= square root of 1+6i squaring both side
(x^2 -y^2)+i2xy=1-36+12i=-35+12i
by comparison
(x^2 -y^2)=-35 and 2xy=12 means xy=6 than y=6/x
x^2-36/x^2=-35
x^4-36/x^2=-35
x^4-36=-35x^2
X^4+35x^2-36=0 let x^2=k than x^4=k^2
k^2+35k-36=0
k^2-36k+k-36=0
(k+1)(k-36)=0
k=-1 or k=36
x^2=-1 means x=i or x^2=36 neglecting value of x=i as x is real value
x=6 or x=-6
than y=6/6 or y=6/-6
y=1 0r y=-1
square root ill be -6+i or -6-i or 6+i or 6-i
answer
6+i
6-i
-6-i
-6+i
Answer by ikleyn(52748)  (Show Source):
You can put this solution on YOUR website! .
The solution by tutor @dkppathak is INCORRECT starting from its second line to the end.
I came to provide a correct solution.
Let x+iy= square root of 1+6i. IT MEANS
(x^2 -y^2) + i2xy = 1 + 6i
by comparison
(x^2 -y^2) = 1 and 2xy = 6 means xy= 3 then y= 3/x
x^2 - 9/x^2 = 1
x^4 - 9 = x^2
x^4 - x^2 - 9 = 0 let x^2=k then x^4=k^2
k^2 - k - 9 = 0
 =  = 
"k" can not be negative, since k = x^2 is the square of the real number.
Hence, k =  .
It implies x = +/-  = +/-  .
To value x = + , corresponds y = 3/x =  =  .
To value x = - , corresponds y = 3/x =  =  .
ANSWER. Square root of 1 + 6i has two values x + iy, where
(x,y) = ( , ) and
(x,y) = (  , ).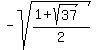
Solved.
------------------
See the lesson
- How to take a square root of a complex number
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
