.
Solve: |z| + z = 2 + i , where z is a complex no.
!~~~~~~~~~~~~~~~~~~
Looking into equation, you can momentarily conclude that the imaginary part of z is i; in other words,
z = a + i, where "a" is a real nnumber.
Then |z| = 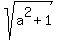 , and the original equation implies for the real parts
, and the original equation implies for the real parts
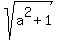 + a = 2,
+ a = 2,
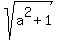 = 2 - a, then squaring both sides
= 2 - a, then squaring both sides
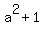 =
= 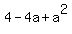 ,
1 = 4 - 4a,
4a = 4-1 = 3 ====> a =
,
1 = 4 - 4a,
4a = 4-1 = 3 ====> a =  .
Answer. z =
.
Answer. z = 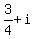 .
.
Solved.