Question 1116414: find all the solutions in the complex numbers, of z^4 + z^3 + z^2 + z + 1 = 0.
use: (1-r)(1+r+r^2+...+r^n)=1-r^(n+1)
which of the solutions are conjugates?
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
According to the formula for the sum of a geometric progression,
 = =  It is the same as
It is the same as
 = = 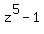 . (*)
(and the formula, which is the hint to your problem, says the same).
From the formula (*), every zero of the polynomial p(z) = z^4 + z^3 + z^2 + z + 1 is the root of the polynomial q(z) = . (*)
(and the formula, which is the hint to your problem, says the same).
From the formula (*), every zero of the polynomial p(z) = z^4 + z^3 + z^2 + z + 1 is the root of the polynomial q(z) = 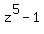 .
In other words, if .
In other words, if  = 0, then = 0, then 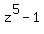 = 0, or, which is the same, = 0, or, which is the same, 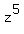 = 1.
Thus every root of the polynomial = 1.
Thus every root of the polynomial  is the complex root of the degree 5 of 1.
And vice versa, every root of the degree 5 of 1, different from 1, is the root of the polynomial is the complex root of the degree 5 of 1.
And vice versa, every root of the degree 5 of 1, different from 1, is the root of the polynomial  . It follows from the formula (*).
Thus the four roots of the polynomial . It follows from the formula (*).
Thus the four roots of the polynomial  are all complex root of degree 5 of 1, different of 1.
OK, very good.
From complex number theory, you can conclude then that these roots have the form are all complex root of degree 5 of 1, different of 1.
OK, very good.
From complex number theory, you can conclude then that these roots have the form
 = =  , where k = 1, 2, 3, 4.
Geometrically, these four complex numbers are vertices of the regular pentagon of the radius 1 centered at (0,0), the origin of the complex plane.
These four roots are vertices of the regular polygon, different of its vertex (1,0).
Of these roots, , where k = 1, 2, 3, 4.
Geometrically, these four complex numbers are vertices of the regular pentagon of the radius 1 centered at (0,0), the origin of the complex plane.
These four roots are vertices of the regular polygon, different of its vertex (1,0).
Of these roots,  is conjugate to is conjugate to  and and  is conjugate to is conjugate to  . .
------------------
Solved, answered and explained.
================
On complex numbers, see the lessons
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
- Solved problems on taking roots of complex numbers
- Solved problems on arithmetic operations on complex numbers
- Solved problem on taking square root of complex number
- Miscellaneous problems on complex numbers
- Advanced problem on complex numbers
- Solved problems on de'Moivre formula
- A curious example of an equation in complex numbers which HAS NO a solution
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|