Question 1116154: How do I find all the values to the following?
1) i^0.25
2) (1+sqrt(3)i)^(1/3)
3) (i-1)^0.5
4) ((9i)/(1+i))^(1/6)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The 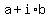 form of complex numbers is not useful for calculating products, powers, and roots. form of complex numbers is not useful for calculating products, powers, and roots.
For those purposes the polar, or trigonometric, or exponential forms are much more useful.
For example, 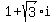 can be written using can be written using
its absolute value or modulus,  , ,
and its argument  such that such that  . .
We could say  to keep it simple, or to keep it simple, or  if you must use radians. if you must use radians.
You can write 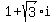 as as 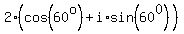 or as or as 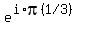 . .
All you need to remember is that when multiplying complex numbers,
absolute values multiply, and arguments add up.
2) So, the solutions to 
are numbers of the form 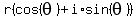 such that such that
 . .
That means that  <--> <--> , ,
and 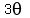 is is  or a coterminal angle. or a coterminal angle.
So, the possibilities for  between between  and and  are are
 --> -->  , ,
 --> -->  , ,
and  --> -->  . .
Approximate values are
 , ,
so we could write the answers as
 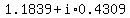
 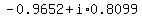
 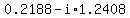
1) The solutions to 
are four fourth roots of 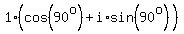 with with
 and and  with with  . .
That means     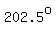  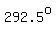 . .
The approximate values of sine and cosine for those angles are:

So, the four complex values of 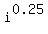 are are
 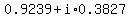 , ,
 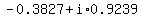
 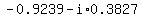 , and , and
 
3)  has 2 values, with has 2 values, with
 and and  with with  . .
That means  with with  , meaning , meaning  or or  . .
Approximate values for sine and cosine of those angles are
 , ,
so we could write the answers as
 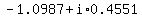 , and , and
 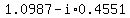 . .
4)  and and  , ,
so their ratio can be calculated as
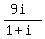  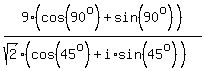  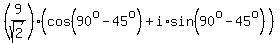  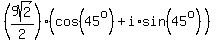
Another way to calculate that quotient is using the conjugate of the denominator:
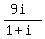  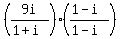  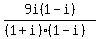      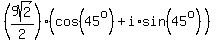 . .
Then,
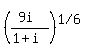  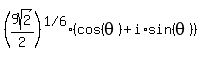 , ,
where  with with  . .
That means
  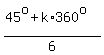  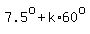 . .
 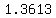 . .
Approximate values for sine and cosine of those angles are

So, the six complex values of 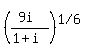 are are
 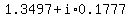 , ,
 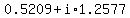 , ,
 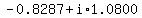 , ,
 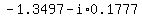 , ,
 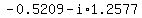 , and , and
 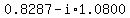 . .
|
|
|