Question 1112242: Show that for all real values of 'a' greater than 4,x Squared-2x+a=3 will have non-real roots
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! in the quadratic formula  one can look at the discriminate
 to figure out what type of roots there will be:
If this value is negative, then the roots are complex (in conjugate pairs)
if this value is zero, then there is a real root, and it has multiplicity 2.
if the value is positive, then there are two unique real roots.
 —> discriminate is  = 
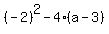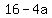
Complex roots will occur when
—
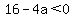
Ans: Complex roots will occur when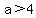 
—
—————————————————————————————————
Dear student,
I did not answer your question twice. The 'a' in the top part where I discuss the discriminate is from the standard form of a quadratic equation  (a is the coefficient of the x^2 term) which I failed to write down for some reason. The 'a' in the question you posted is part of the constant term (c) in that expression.
To make it clear, let's re-write the question as follows: " For what values of 'v' does  have non-real roots?"
Compare this with the standard form of the quadratic you will see a=1, b=-2, c=v-3 (here a,b,c refer to the standard form of the quadratic equation).
Now plug into the discriminate, D, D =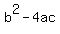 
D =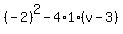 
D =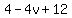 
D =  —> this means when 16-4v < 0 there are non-real (complex) roots.
16-4v < 0
16 < 4v
4 < v
v > 4 <<<< done. I used 'v' instead of 'a' to avoid confusion with the standard form of the quadratic equation.
I hope this helps.
|
|
|
