Question 1046469: Hello,
I need help with the following math problem:
Find all complex numbers 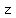 such that (the link to the equation is below): such that (the link to the equation is below):
http://latex.artofproblemsolving.com/c/d/8/cd807464a7f54a2312083e11bdde20cc2ef4ee83.png
Please give a detailed explanation of how to solve this problem.
Thank you,
Nicole
Answer by ikleyn(52906)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello,
 Could you please help me with the following math problem: Could you please help me with the following math problem:
Find all complex numbers 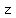 such that (the link to the equation is below): such that (the link to the equation is below):
http://latex.artofproblemsolving.com/c/d/8/cd807464a7f54a2312083e11bdde20cc2ef4ee83.png
Thank you,
Nicole
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
|z|^2 - 2*conj(z) + i*z = 2i. (1) (conj(z) means z-conjugated . . . )
Let z = x + yi, where "x" and "y" are unknown real numbers.
Then
|z|^2 =  (real number);
2*conj(z) = 2x - 2yi;
i*z = -y +x*i (why? Try to understand it on your own. It is elementary . . . )
Now substitute all this stuff into (1). You will get (real number);
2*conj(z) = 2x - 2yi;
i*z = -y +x*i (why? Try to understand it on your own. It is elementary . . . )
Now substitute all this stuff into (1). You will get
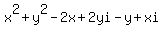 = =  . (2)
It is an equality of complex numbers. It means that their real parts are equal and imaginary parts are equal.
In other words, you have these two equations, first for real parts and the second for imaginary parts . (2)
It is an equality of complex numbers. It means that their real parts are equal and imaginary parts are equal.
In other words, you have these two equations, first for real parts and the second for imaginary parts
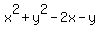 = 0, (3) ( which represents a circle . . . ) and
2y + x = 2. (4) ( which represents a straight line )
Now you need to solve this system and to find "x" and "y" (the intersection points).
I don't want to deprive you, Nicole, the pleasure to do it on your own.
Can you complete it?
If not, let me know, I will help you in it.
In this case, send me a message through the "Thank you" window, and do not forget to mention
the ID number of the problem ( 1046469 ) in order for I could identify it.
Good luck! = 0, (3) ( which represents a circle . . . ) and
2y + x = 2. (4) ( which represents a straight line )
Now you need to solve this system and to find "x" and "y" (the intersection points).
I don't want to deprive you, Nicole, the pleasure to do it on your own.
Can you complete it?
If not, let me know, I will help you in it.
In this case, send me a message through the "Thank you" window, and do not forget to mention
the ID number of the problem ( 1046469 ) in order for I could identify it.
Good luck!
There is a bunch of my lessons on complex numbers
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
in this site.
I think that some of them might be useful to you.
|
|
|