Question 1043673: Please help me solve (12i)^1/2 to a+bi form
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me solve (12i)^1/2 to a+bi form
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The general procedure on how to find the roots of a complex number is explained in the lesson
- How to take a root of a complex number
in this site.
If you just are familiar with complex numbers, operations on them, complex plane, trigonometric form of complex numbers -
- then you will be able to understand it.
If you are not familiar with this material, then you can learn on complex numbers from these lessons
- Complex numbers and arithmetic operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
After this introduction, let me briefly explain you how to solve your problem.
So, you need to find 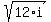 .
Write 12*i in the trigonometric form z = .
Write 12*i in the trigonometric form z = 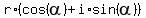 ,
where "r" is the modulus and ,
where "r" is the modulus and  is the argument (polar angle).
In your case, z = 12*i in trigonometric form is z = is the argument (polar angle).
In your case, z = 12*i in trigonometric form is z = 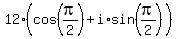 , so the modulus is r = 12 and the polar angle is , so the modulus is r = 12 and the polar angle is  = =  .
Now, to find the square root of this complex number, you have
1. to take a square root of the modulus: .
Now, to find the square root of this complex number, you have
1. to take a square root of the modulus: 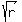 = =  = =  .
2. to divide the argument (polar angle) by 2: .
2. to divide the argument (polar angle) by 2: 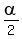 = = 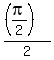 = =  .
3. to consider the complex number .
3. to consider the complex number  = = 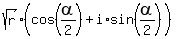 , which is in your case , which is in your case
 = = 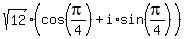 = = 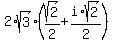 = = 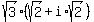 = =  = = 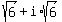 .
It is one of the two complex roots. // Notice that the modulus of .
It is one of the two complex roots. // Notice that the modulus of  is is 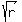 and the argument is and the argument is 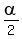 = =  .
// Also notice that the final expression for .
// Also notice that the final expression for  is just a + bi form.
4. to get the second root is just a + bi form.
4. to get the second root  in trigonometric form, you have to use the same modulus as in trigonometric form, you have to use the same modulus as  has, namely has, namely 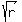 , but use another
argument, which this time is , but use another
argument, which this time is 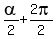 = = 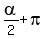 .
Then your .
Then your  = = 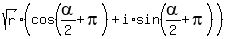 = = 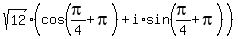 = = 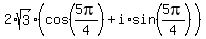 =
= =
= 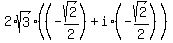 = = 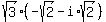 = = 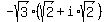 = =  = = 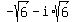 .
// Notice that .
// Notice that  = = 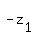 .
// All this long way with .
// All this long way with  lead us to the opposite number to lead us to the opposite number to  .
// But now you know all the procedure, how it works for square roots of complex numbers.
// Surely, it may seem too complex, at the first glance.
// But there is a powerful symmetry in it, which work nicely for all n > 2.
// If you read the lessons I recommended you, you will be able to learn its real power and beauty.
Answer. .
// But now you know all the procedure, how it works for square roots of complex numbers.
// Surely, it may seem too complex, at the first glance.
// But there is a powerful symmetry in it, which work nicely for all n > 2.
// If you read the lessons I recommended you, you will be able to learn its real power and beauty.
Answer. 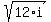 has two values: has two values:  = = 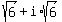 and and  = = 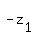 = = 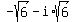 . .
|
|
|