Question 878321: Determine the inequation that would define this region: all points on and below the absolute value function with zeros at x=4 and x=10, and a vertex at (7,2).
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine the inequation that would define this region: all points on and below the absolute value function with zeros at x=4 and x=10, and a vertex at (7,2).
Here is the graph of what you want:
 First we get the equation of the boundary line.
Absolute value functions have the form
y = a|x-h|+k
Where (h,k) is the vertex. If "a" is positive the graph will open
upward and if it is negative it will open downward. So we expect
"a" to be negative.
Since the vertex is (h,k) = (7,2) we substitute those values:
y = a|x-7|+2
To find "a" we substitute any point other than the vertex.
Since we know it goes through (4,0), we substitute (x,y) = (4,0)
y = a|x-7|+2
0 = a|4-7|+2
0 = a|-3|+2
0 = a(3)+2
0 = 3a+2
-2 = 3a
First we get the equation of the boundary line.
Absolute value functions have the form
y = a|x-h|+k
Where (h,k) is the vertex. If "a" is positive the graph will open
upward and if it is negative it will open downward. So we expect
"a" to be negative.
Since the vertex is (h,k) = (7,2) we substitute those values:
y = a|x-7|+2
To find "a" we substitute any point other than the vertex.
Since we know it goes through (4,0), we substitute (x,y) = (4,0)
y = a|x-7|+2
0 = a|4-7|+2
0 = a|-3|+2
0 = a(3)+2
0 = 3a+2
-2 = 3a
 = a
Substitute that for 'a' in
y = = a
Substitute that for 'a' in
y =  |x-7|+2
Now since the lower area is shaded, and the graph
includes the boundary line, we use |x-7|+2
Now since the lower area is shaded, and the graph
includes the boundary line, we use  . .
  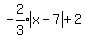 Edwin
Edwin
|
|
|