This is giving me troubles please help me. Solve 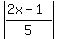 >
> 
Rules for getting rid of absolute value symbols in inequalities,
The word "EXPRESSION" refers to whatever expression is between the
absolute value symbols:
1. |EXPRESSION| < A is equivalent to: -A < EXPRESSION < A
2. |EXPRESSION| < A ie equivalent to: -A < EXPRESSION < A
3. |EXPRESSION| > A ie equivalent to: EXPRESSION < -A OR EXPRESSION > A
04. |EXPRESSION| > A ie equivalent to: EXPRESSION < -A OR EXPRESSION > A
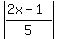 >
>  This is case 4 with EXPRESSION =
This is case 4 with EXPRESSION = 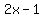 and A =
and A =  Thus it is equivalent to:
Thus it is equivalent to:
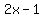 <
< 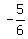 OR
OR 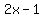 >
>  Multiply both sides of both inequalities by 30 to clear of fractions:
Multiply both sides of both inequalities by 30 to clear of fractions:
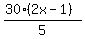 <
< 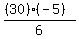 OR
OR 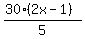 >
> 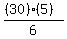 6(2x - 1) < -25 OR 6(2x - 1) > 25
12x - 6 < -25 OR 12x - 6 > 25
12x < -19 OR 12x > 31
x <
6(2x - 1) < -25 OR 6(2x - 1) > 25
12x - 6 < -25 OR 12x - 6 > 25
12x < -19 OR 12x > 31
x < 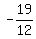 OR x >
OR x > 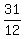 Make three number lines:
Draw three number lines with a closed circle
at the boundary points (closed because it's
"<" OR ">" and not "<" OR ">"):
x <
Make three number lines:
Draw three number lines with a closed circle
at the boundary points (closed because it's
"<" OR ">" and not "<" OR ">"):
x <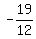 -----------l-------------l----------
-----------l-------------l----------
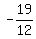
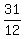 x >
x >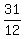 -----------l-------------l----------
-----------l-------------l----------
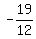
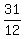 x <
x <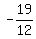 OR x >
OR x > 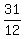 -----------l-------------l----------
-----------l-------------l----------
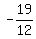
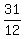 Shade the first one to the left of
Shade the first one to the left of 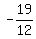 , because
"less than" is "left":
x <
, because
"less than" is "left":
x <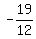 <==========l-------------l----------
<==========l-------------l----------
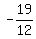
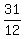 Shade the second one to the right of
Shade the second one to the right of 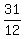 , because
"greater than" is "right":
x >
, because
"greater than" is "right":
x > 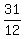 -----------l-------------l==========>
-----------l-------------l==========>
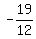
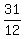 Now since the word between the inequalities is "OR"
and not "AND", we shade all parts of the final
number line if it is shaded on the first one OR if
it is shaded on the second one.
So the final number line is:
x <
Now since the word between the inequalities is "OR"
and not "AND", we shade all parts of the final
number line if it is shaded on the first one OR if
it is shaded on the second one.
So the final number line is:
x <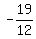 or x >
or x >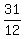 <==========l-------------l==========>
<==========l-------------l==========>
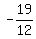
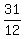 Now we imagine that there is a "negative infinity"
on the far left and an "infinity" on the far right.
So the interval notation is
(-oo,
Now we imagine that there is a "negative infinity"
on the far left and an "infinity" on the far right.
So the interval notation is
(-oo, 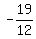 ] U [
] U [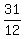 , oo)
Edwin
, oo)
Edwin