Question 294858: x(|x-2|)>=0. x-2 is an absolute value.
I thought the answer was x= all real numbers, but the x on the outside of the bracket messes that up. How do I approach this?
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolute value problems are really two problems in one.
Positive solution (where  ): ):

This is true when  and also when and also when 
.
.
.
Negative solution (where  ): ):


Break up the region into three regions,
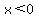
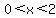

and test a point to check the inequality
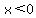 , , 


No, not in the valid region.
.
.
.
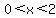 , , 


Yes, in the valid region.
.
.
.
 , , 


No, not in the valid region.
So from the negative solution, the valid region would be (0,2).
Put together with  and and  , then the valid region is, , then the valid region is,
( ) )
|
|
|