Graph each Absolute Value equation by writting two linear equations.
One linear equation is gotten from the case
when what is between the absolute value bars,
3x+6, is negative, that is, less than 0.
The other linear equation is gotten from the
case when what is between the absolute value
bars, 3x+6, is either positive or zero, that
is, greater than or equal to 0.
The first linear equation is gotten when 3x+6
is negative, but if 3x+6 is negative, then if
we multiply 3x+6 by -1, then it will become
positive, and so -1(3x+6) will be positive,
and that will be the absolute value of 3x+6,
when 3x+6 is negative. So the first linear
equation is
or
.
So we draw the graph of that line:
However, since we are requiring that
what is between the absolute value
bars, 3x+6, is less than 0, we must
only use the part of that line where
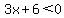. So we solve that:
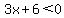
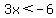
Therefore we must chop off the line
to the RIGHT of where x is equal to
-2. So the graph is only this part
of the line:
and it DOES NOT include the point
(-2,0).
-----------------
Now The second linear equation is gotten
when 3x+6 is positive or zero, and if 3x+6
is positive or zero, then we do not need
abslute value bars at all. That is, when
3x+6 is positive or zero, the absolute
value of 3x+6 is simply 3x+6! So the
second linear equation is just:
So we draw the graph of that line on
the same set of axes:
However, since we are requiring that
what is between the absolute value
bars, 3x+6, is greater than or equal
to 0, we must only use the part of
that line where 
. So
we solve that:
Therefore we must chop off that line
to the LEFT of where x is equal to -2.
So the FINAL graph is only this V-shaped
graph:
and and the part slanting up to the right
DOES include the point (-2,0),
So the absolute value equation
can be written as the piecewise function
without using any absolute value bars!
Edwin
