SOLUTION: A t-shirt design company is dying purple shirts for a school club. The shirts came out too light so the company needs to add more pure blue dye to the mixture to get a darker purp

Let V be the volume to drain off from 54 gallons of the 27% solution.


Step 1:  Draining.  After draining,  you have (54-V) gallons of the 27% acid solution.



Step 2:  Replacing.  Then you add V gallons of the pure blue dye (the replacing step).

                     After the replacing,  you have the same total liquid volume of 54 gallons.


It contains  0.27*(54-V) + V   of pure blue dye.



So, your "concentration equation" is


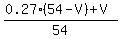     = 0.4.    (1)



At this point, the setup is done and completed.



Now you need to solve your basic equation  (1).

As the first step, multiply both sides by 80, and then simplify


    0.27*(54-V) + V = 0.4*54

    14.58 - 0.27V + V = 21.6

    0.73V = 21.6 - 14.58 = 7.02

    V = 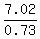 = 9.616.


ANSWER.  9.616 gallons of the 27% solution should be drained and replaced by the pure blue duy.


CHECK.    = 0.4.    ! Precisely correct !