Question 1139438: |3(|x-5|)-8|> 5
Solution set and graph please
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
| 3*(|x-5|)-8 | > 5
is equivalent to the system of two inequalities
3*|x-5| - 8 > 5 (a)
OR
3*|x-5| - 8 < -5 (b)
Notice this service word "OR" in the formulation of the system.
It means that you should solve each inequality and then the final solution set to the system is the UNION of the two individual solution sets.
Now I will solve inequalities (a) and (b) separately, and will start with inequality (a).
3*|x-5| - 8 > 5 (a)
is the same as
3*|x-5| > 5 + 8 = 13
is equivalent to (after dividing all the three terms of the inequality by 3)
|x-5| > 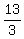 .
The solutions to the last inequality are those values of x (those numbers or points in the number line)
that are remoted from the point x= 5 farther than .
The solutions to the last inequality are those values of x (those numbers or points in the number line)
that are remoted from the point x= 5 farther than 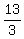 units.
Obviously, these points (numbers, solutions) are
x < 5 - units.
Obviously, these points (numbers, solutions) are
x < 5 - 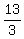 and/or x > 5 + and/or x > 5 + 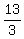 .
Next I will solve inequality (b).
3*|x-5| - 8 < -5 (b)
is the same as
3*|x-5| < -5 + 8 = 3
is equivalent to (after dividing all the three terms of the inequality by 2)
|x-5| < 1.
The solutions to the last inequality are those values of x (those numbers or points in the number line)
that are remoted from the point x= 5 closer than 1 units.
Obviously, these points (numbers, solutions) are 4 < x < 6, or the interval (4,6).
After completing solving inequalities (a) and (b) we have the
ANSWER. The solution set to the original inequality is the union of three intervals x < 5 - .
Next I will solve inequality (b).
3*|x-5| - 8 < -5 (b)
is the same as
3*|x-5| < -5 + 8 = 3
is equivalent to (after dividing all the three terms of the inequality by 2)
|x-5| < 1.
The solutions to the last inequality are those values of x (those numbers or points in the number line)
that are remoted from the point x= 5 closer than 1 units.
Obviously, these points (numbers, solutions) are 4 < x < 6, or the interval (4,6).
After completing solving inequalities (a) and (b) we have the
ANSWER. The solution set to the original inequality is the union of three intervals x < 5 - 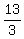 , 4 < x < 6, x > 5 + , 4 < x < 6, x > 5 + 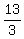 . .
Solved, answered, explained and completed.
|
|
|