.
The integer number 130 has this decomposition into the product of these prime numbers:
130 =  .
. .
. =
= 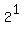 .
.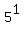 .
.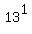 .
Note that the indexes are 1 for 2, 1 for 5 and 1 for 13.
Now add 1 to each of the three indexes:
1 + 1 = 2 (for 2);
1 + 1 = 2 (for 5);
1 + 1 = 2 (for 13).
Now the number of all divisors for 130 (including 1 and including 130 itself) is the product 2*2*2 = 8.
They are
1 =
.
Note that the indexes are 1 for 2, 1 for 5 and 1 for 13.
Now add 1 to each of the three indexes:
1 + 1 = 2 (for 2);
1 + 1 = 2 (for 5);
1 + 1 = 2 (for 13).
Now the number of all divisors for 130 (including 1 and including 130 itself) is the product 2*2*2 = 8.
They are
1 = 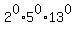 ,
2 =
,
2 = 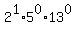 ,
5 =
,
5 = 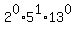 ,
10 =
,
10 = 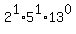 ,
13 =
,
13 = 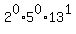 ,
26 =
,
26 = 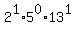 ,
65 =
,
65 = 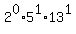 ,
130 =
,
130 = 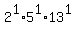 .
.
The answer to your problem is the option a): there are 8 divisors.