Question 1070609: Rewrite without absolute value sign for differe nt values of x:
y=−(2x+5)−2x−5
1. if x<−2.5
2. if x>2.5
3. if −2.5≤x≤2.5
PLZ ANSWER BEFORE 5:30 EST
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your post did not have any absolute value sign,
so the question did not make sense,
and no one could answer it.
I assume that the expressions inside absolute value were
 and/or and/or  . .
If so, the way to figure out the answer is
to figure out ways to write the absolute value expressions
without the absolute value symbols/signs.
You can practice algebra,
solving inequalities as I show below.
You know that if what is inside the absolute value sign
is positive or even zero,
the absolute value sign is not needed
Otherwise, the expression inside the absolute value is negative,
and to get the absolute value you have to change around all plus and minus signs,
even the ones we do not write because they are at the beginning,
as in  . .
 for for  and only for those numbers,so and only for those numbers,so
 for for  , and , and
otherwise 
 for for  and only for those values of and only for those values of  , so , so
 for for  ,and ,and
otherwise  . .
TRICK: If inequalities give you a stress headache,
or you are pressed for time,
or you get anxious and unsure of your solutions,
you can figure out in which of the three cases the expression will be positive or negative
by using test values for x that match each of those three cases.
For example, for case 1. 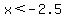 you could use you could use 
If you substitute that into the expressions,you find that
 and and  , ,
so both expressions are negative.
That trick works in this case because
you were given the conditions for the three cases,
and because the expressions in the absolute value were linear expressions.
Ět is sort of cheating, but speeds the work.
SOLVING THE INEQUALITIES WAY:
1. If 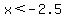 , as for example when , as for example when  or or  , ,
of course  and and 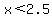 , ,
so you know what expression without absolute value sign to use
to replace each absolute value part.
2. If  , of course , of course 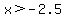 , ,
and you know what to replace for each absolute value part.
3. If 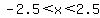 , as happens for , as happens for  , ,
then 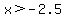 and and 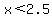 and you can figure out what to and you can figure out what to
replace cor each absolute value part.
|
|
|