SOLUTION: I need a two digit number which after reversing I should get a two digit number which will be twice the previous number. Which is the number?

Algebra ->  Absolute-value -> SOLUTION: I need a two digit number which after reversing I should get a two digit number which will be twice the previous number. Which is the number?      Log On


   

Question 1040376: I need a two digit number which after reversing I should get a two digit number which will be twice the previous number.
Which is the number?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
10t%2Bu=2%2810u%2Bt%29

Simplify and make a two-dimensional cartesian graph. This will be a line and you can identify any points with only positive integer coordinates between 0 and 9.

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

I need a two digit number which after reversing I should get a two digit number which will be twice the previous number.
Which is the number?
Let tens and units digits be T, and U, respectively

Then number is: 10T + U, and when reversed is: 10U + T

We then get: 10U + T = 2(10T + U)

10U + T = 20T + 2U 

20T - T = 10U - 2U

19T = 8U

T, or tens digit = 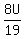8U%2F19

There's no digit, from 1 - 9, that when multiplied by 8, results in a double-digit number that is a MULTIPLE of 19.

Therefore, there is: highlight_green%28matrix%281%2C2%2C+NO%2C+SOLUTION%29%29