This Lesson (HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 3) was created by by ikleyn(52776)   : View Source, ShowAbout ikleyn:
How to solve equations containing Linear Terms under the Absolute Value sign. Lesson 3
In this lesson you will see how to solve equations containing Linear Terms under the Absolute Value sign.
We consider, one after the other, the solution procedure for the following examples:
a)  = =  - -  ; ;
b)  = =  - -  ; ;
c) 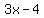 = =  - -  ; ;
d)  = =  - -  ; ;
e)  = =  - -  ; ;
f)  = =  - -  . .
The starting lessons in this series are
How to solve equations containing Linear Terms under the Absolute Value sign. Lesson 1
How to solve equations containing Linear Terms under the Absolute Value sign. Lesson 2
where simple cases are considered.
The goal is to get you acquainted with the different typical situations you can meet solving this kind of problems.
When you learn how to solve these equations, you will easily proceed in many other cases.
Problem 1
Solve absolute value equation a)  = =  - - (1); (1);
Solve absolute value equation b)  = =  - - (2); (2);
Solve absolute value equation c) 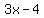 = =  - - (3); (3);
Solve absolute value equation d)  = =  - - (4); (4);
Solve absolute value equation e)  = =  - - (5); (5);
Solve absolute value equation f)  = =  - - (6). (6).
Solution to 1a)
We have two groups of the terms under the Modulus sign. The first group is  , the second group is , the second group is  . .
For the first group, according to the definition of Absolute Value,
 = =  , if , if  >= 0, and >= 0, and
 = = 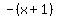 , if , if  < 0. < 0.
So, the Modulus  is the linear function is the linear function  over the range over the range
 >= >=  , and the linear function , and the linear function 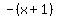 over the range over the range  < <  . .
Similarly, the Modulus  is the linear function is the linear function  over the range over the range
 >= >=  , and the linear function , and the linear function 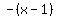 over the range over the range  < <  . .
Now, we can divide the entire set of real numbers into adjacent ranges
 , ,  and and 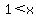 and combine the respective linear and combine the respective linear
functions over these ranges.
In this way, you will get
 - -  = = 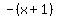 - [ - [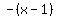 ] = ] =  over over  <= <=  , ,
 - -  = = 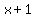 - [ - [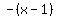 ] = ] =  over over  , and , and
 - -  = = 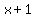 - -  = =  over over 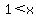 . .
|

Figure 1a. Plot of the function
 = =  - - 
|

Figure 1a'. To the solution
 = =  - - 
|
The resulting plot of the function  = =  - -  is shown in Figure 1a. It consists of three piecewise straight lines. is shown in Figure 1a. It consists of three piecewise straight lines.
Thus, the equation  = =  - -  which we should solve is equivalent to the three equations over the respective ranges: which we should solve is equivalent to the three equations over the respective ranges:
 = =  - -  over over  <= <=  , which is , which is  = =  over over  <= <=  , (7) , (7)
 = =  - -  over 1 < over 1 <  <= <=  , which is , which is  = =  over over  < <  <= <=  , (8) , (8)
 = =  - -  over over  < <  , which is , which is  = =  over over  < <  . (9) . (9)
Equation (7) has the solution  = =  . This solution belongs to the range . This solution belongs to the range  <= <=  and satisfies all requirements. and satisfies all requirements.
Equation (8) has the solution  = =  . This solution belongs to the range . This solution belongs to the range  < <  <= <=  and satisfies all requirements. and satisfies all requirements.
Equation (9) has the solution  = =  . This solution belongs to the range . This solution belongs to the range  < <  and satisfies all requirements. and satisfies all requirements.
So, the equation (1) has three solutions  = =  , ,  = =  and and  = =  . .
In Figure 1a' the plot of the function  = =  - -  is presented by the black lines. The red line represents the linear function is presented by the black lines. The red line represents the linear function  = =  . .
The three intersection points represent the three solutions we just found.
Solution 1b)
We just derived in the solution to Problem 1a) above that
 - -  = =  over over  <= <=  , ,
 - -  = =  over over  , ,
 - -  = =  over over 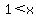 . .
Hence, the equation  = =  - -  which we should solve which we should solve
is equivalent to the three equations over the respective ranges:
 = =  - -  over over  <= <=  , which is , which is  = =  over over  <= <=  , (10) , (10)
 = =  - -  over 1 < over 1 <  <= <=  , which is , which is  = =  over over  < <  <= <=  , (11) , (11)
 = =  - -  over over  < <  , which is , which is  = =  over over  < <  . (12) . (12)
|

Figure 1b. To the solution
 = =  - - 
|
Equation (10) has the solution  = =  . This solution belongs to the range . This solution belongs to the range  <= <=  and satisfies all requirements. and satisfies all requirements.
Equation (11) has the solution  = =  . This solution belongs to the range . This solution belongs to the range  < <  <= <=  , and satisfies all requirements. , and satisfies all requirements.
Equation (12) has the root  = =  . This root does not belong to the range . This root does not belong to the range  < <  , hence, does not satisfy all requirements. , hence, does not satisfy all requirements.
So, the equation (2) has two solutions  = =  and and  = =  . .
In Figure 1b the plot of the function  = =  - -  is presented by the black lines. The red line represents the linear function is presented by the black lines. The red line represents the linear function  = =  . .
The two intersection points represent the two solutions we just found.
Solution 1c)
We just derived in the solution to Problem 1a) above that
 - -  = =  over over  <= <=  , ,
 - -  = =  over over  , ,
 - -  = =  over over 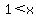 . .
Hence, the equation 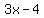 = =  - -  which we should solve which we should solve
is equivalent to the three equations over the respective ranges:
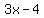 = =  - -  over over  <= <=  , which is , which is 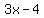 = =  over over  <= <=  , (13) , (13)
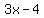 = =  - -  over 1 < over 1 <  <= <=  , which is , which is 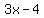 = =  over over  < <  <= <=  , (14) , (14)
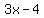 = =  - -  over over  < <  , which is , which is 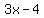 = =  over over  < <  . (15) . (15)
|

Figure 1c. To the solution
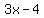 = =  - - 
|
Equation (13) has the root  = =  . This root does not belong to the range . This root does not belong to the range  <= <=  , and, hence, does not satisfy all requirements. , and, hence, does not satisfy all requirements.
Equation (14) has the root  = =  . This root does not belong to the range . This root does not belong to the range  < <  <= <=  , and, hence, does not satisfy all requirements. , and, hence, does not satisfy all requirements.
Equation (15) has the root  = =  . This root belongs to the range . This root belongs to the range  < <  , and, hence, satisfy all requirements. , and, hence, satisfy all requirements.
So, the equation (3) has the unique solution  = =  . .
In Figure 1c the plot of the function  = =  - -  is presented by the black lines. The red line represents the linear function is presented by the black lines. The red line represents the linear function  = = 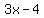 . .
The two intersection points represent the two solutions we just found.
Solution 1d)
We just derived in the solution to Problem 1a) above that
 - -  = =  over over  <= <=  , ,
 - -  = =  over over  , ,
 - -  = =  over over 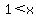 . .
Hence, the equation  = =  - -  which we should solve which we should solve
is equivalent to the three equations over the respective ranges:
 = =  - -  over over  <= <=  , which is , which is  = =  over over  <= <=  , (16) , (16)
 = =  - -  over 1 < over 1 <  <= <=  , which is , which is  = =  over over  < <  <= <=  , (17) , (17)
 = =  - -  over over  < <  , which is , which is  = =  over over  < <  . (18) . (18)
|

Figure 1d. To the solution
 = =  - - 
|
Equation (16) has the root  = =  . This root belongs to the range . This root belongs to the range  <= <=  , and, hence, satisfies all requirements. , and, hence, satisfies all requirements.
Equation (17) is the identity. Every real number  of the range of the range  < <  <= <=  is the solution. So, the equation (17) has infinitely many solutions. is the solution. So, the equation (17) has infinitely many solutions.
Equation (18) has the root  = =  . This root does not belong to the range . This root does not belong to the range  < <  , and, hence, does not satisfy all requirements. , and, hence, does not satisfy all requirements.
So, the equation (4) has infinitely many solutions.
In Figure 1d the plot of the function  = =  - -  is presented by the black lines. The red line represents the linear function is presented by the black lines. The red line represents the linear function  = =  . .
The straight line  = =  coincides with the plot of the function coincides with the plot of the function  = =  - -  over the range over the range  <= <=  <= <=  . .
Solution 1e)
We just derived in the solution to Problem 1a) above that
 - -  = =  over over  <= <=  , ,
 - -  = =  over over  , ,
 - -  = =  over over 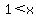 . .
Hence, the equation  = =  - -  which we should solve which we should solve
is equivalent to the three equations over the respective ranges:
 = =  - -  over over  <= <=  , which is , which is  = =  over over  <= <=  , (19) , (19)
 = =  - -  over 1 < over 1 <  <= <=  , which is , which is  = =  over over  < <  <= <=  , (20) , (20)
 = =  - -  over over  < <  , which is , which is  = =  over over  < <  . (21) . (21)
|

Figure 1e. To the solution
 = =  - - 
|
Equation (19) has no solutions.
Equation (20) has the root  = =  . This root belongs to the range . This root belongs to the range  < <  <= <=  and, hence, satisfies all requirements. and, hence, satisfies all requirements.
Equation (21) is the identity. Every real number  of the range of the range  < <  is the solution. So, the equation (21) has infinitely many solutions. is the solution. So, the equation (21) has infinitely many solutions.
Thus, the equation (5) has infinitely many solutions.
In Figure 1e the plot of the function  = =  - -  is presented by the black lines. The red line represents the linear function is presented by the black lines. The red line represents the linear function  = =  . .
The straight line  = =  coincides with the plot of the function coincides with the plot of the function  = =  - -  over the range over the range  <= <=  . .
Solution 1f)
We just derived in the solution to Problem 1a) above that
 - -  = =  over over  <= <=  , ,
 - -  = =  over over  , ,
 - -  = =  over over 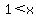 . .
Hence, the equation  = =  - -  which we should solve which we should solve
is equivalent to the three equations over the respective ranges:
 = =  - -  over over  <= <=  , which is , which is  = =  over over  <= <=  , (22) , (22)
 = =  - -  over 1 < over 1 <  <= <=  , which is , which is  = =  over over  < <  <= <=  , (23) , (23)
 = =  - -  over over  < <  , which is , which is  = =  over over  < <  . (24) . (24)
|

Figure 1f. To the solution
 = =  - - 
|
Equation (22) has no solutions.
Equation (23) has no solutions.
Equation (24) has no solutions.
Thus, the equation (6) has no solutions.
In Figure 1f the plot of the function  = =  - -  is presented by the black lines. The red line represents the constant function is presented by the black lines. The red line represents the constant function  = =  . .
There is no intersection point of the plot  = =  - -  and the plot and the plot  = =  . .
Below the plots of the Figure 1a - Figure 1f are presented again for your convenience.

Figure 1a. To the solution  = = 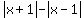
(three roots)
|

Figure 1b. To the solution  = =  - - 
(two roots)
|

Figure 1c. To the solution 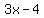 = =  - - 
(one root)
|

Figure 1d. To the solution  = =  - - 
(infinitely many roots)
|

Figure 1e. To the solution  = =  - - 
(infinitely many roots)
|

Figure 1f. To the solution  = =  - - 
(no roots)
|
Note that the strategy of the solution is the same in all examples. It is to break up the entire set of real numbers into sub-domains (ranges)
where the absolute value of linear term is a linear function, and then to solve the corresponding linear equations in each sub-domain (range).
My other lessons on Absolute Value equations in this site are
- Absolute Value equations
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 2
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 4
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 2
See also the lesson OVERVIEW of lessons on Absolute Value equations under the current topic in this site.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 3112 times.
|

