Question 939772: How do I figure out the smallest surface area of a cylinder when I only know what the volume is? the volume is 50,000cm cubed.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you need to design a cylinder with a volume of 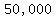  , ,
you could start with
 = radius of the bases of the cylinder, and = radius of the bases of the cylinder, and
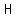 = height of the cylinder, = height of the cylinder,
both in  . .
The volume in  is calculated as is calculated as
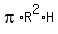 . .
If that volume is 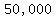  , then , then
 --> --> . .
Now, if you make it a right cylinder
(one with its axis perpendicular to the bases,
the total surface area is calculated as
 . .
Substituting  into the equation above, we get into the equation above, we get



The area as a function of radius of the cylinder
is very large for
very narrow (and very tall) cylinders, and for
very short and very wide) cylinders with the same area
Its graph looks like this
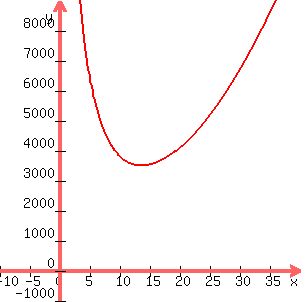
In the middle, there is a value for the radius that makes the surface are as small as possible.
How would you find that value for the radius, and the minimum area?
Maybe you are expected to use a graphing calculator.
Maybe you are studying calculus.
and are expected to calculate the derivative of the function
 , ,
and find the  value where that derivative is zero ans value where that derivative is zero ans  is minimum. is minimum.
The derivative is
 <--> <-->
and that is zero when
 --> --> --> --> --> --> , ,
and the approximate value for the minimum area (in cubic cm)
(when  takes that value) is takes that value) is

|
|
|