|
Question 1207300: A company that manufactures dog food wishes to pack in closed cylindrical tins.
What should be the dimensions of each tin if it is to have a volume of 128πcm³
and the minimum possible surface area?
Found 4 solutions by ikleyn, greenestamps, Edwin McCravy, MathLover1:
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A company that manufactures dog food wishes to pack in closed cylindrical tin's as,
what should be the dimensions of each tin if it is to have a volume of 128π cm³
and the minimum possible surface area.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
As you know, the volume of a cylinder is
V = 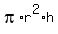 ,
where pi = 3.14, r is the radius and h is the height.
In your case the volume is fixed: ,
where pi = 3.14, r is the radius and h is the height.
In your case the volume is fixed:
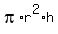 = =  cm^3. (1)
The surface area of a cylinder is
S = cm^3. (1)
The surface area of a cylinder is
S = 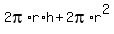 , (2)
and they ask you to find minimum of (2) under the restriction (1).
Using (1), I can rewrite (2) in the form
S(r) = , (2)
and they ask you to find minimum of (2) under the restriction (1).
Using (1), I can rewrite (2) in the form
S(r) = 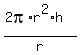 + +  = = 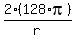 + +  = = 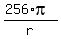 + +  . (3)
The plot below shows the function S(r) = . (3)
The plot below shows the function S(r) = 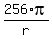 + +  , and you can clearly see that it has the minimum. , and you can clearly see that it has the minimum.
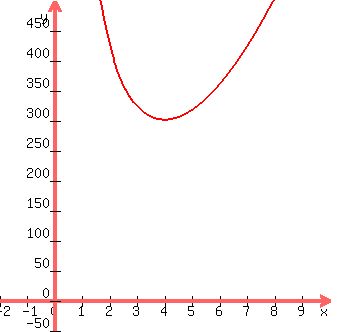 Plot y =
Plot y = 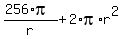 To find the minimum, use Calculus: differentiate the function to get
S'(r) =
To find the minimum, use Calculus: differentiate the function to get
S'(r) = 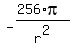 + + 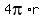 = = 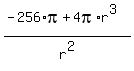 and equate it to zero.
S'(r) = 0 leads you to equation
and equate it to zero.
S'(r) = 0 leads you to equation 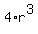 = =  , which gives
r = , which gives
r = 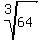 = 4 cm.
Answer. r = 4 cm, h = = 4 cm.
Answer. r = 4 cm, h = 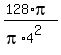 = 8 cm gives the minimum of the surface area. = 8 cm gives the minimum of the surface area.
Solved.
Answer by greenestamps(13258)   (Show Source): (Show Source):
Answer by Edwin McCravy(20077)   (Show Source): (Show Source):
Answer by MathLover1(20854)   (Show Source): (Show Source):
|
|
|
| |