|
Question 1195840: A tinsmith wants to make a small windowsill planter from a 38cm x 22cm sheet of copper. She’ll form it by cutting equally sized squares from each of the four corners of the sheet, folding up the resulting flaps to form the sides of the planter, and then shouldering the four vertical edges. What is the maximum possible volume of the planter? Round your answer to the nearest whole number.
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A tinsmith wants to make a small windowsill planter from a 38cm x 22cm sheet of copper.
She’ll form it by cutting equally sized squares from each of the four corners of the sheet,
folding up the resulting flaps to form the sides of the planter,
and then shouldering the four vertical edges.
What is the maximum possible volume of the planter? Round your answer to the nearest whole number.
~~~~~~~~~~~~~~~~~~
After folding up the resulting flaps, the base of the planter has dimensions
(38-2x) cm by (22-2x) cm and the height is x cm.
Thus the volume is
V(x) = (38-2x)*(22-2x)*x cm^3.
To find the maximum V(x), take the derivative and equate it to zero
0 = V'(x) = -2*(22-2x)*x + (38-2x)*(-2)*x + (38-2x)*(22-2x) =
= -44x + 4x^2 - 76x + 4x^2 + 38*22 - 44x - 76x + 4x^2 =
= 12x^2 - 240x + 836.
It gives
3x^2 - 60x + 209 = 0.
The roots are (use the quadratic formula)
 = = 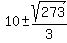 ,
or ,
or
 = 15.5076, = 15.5076,  = 4.49243.
The larger root is TOO big and, therefore, is not the solution to the problem.
The other value, 4.49243, is the approximate solution for x.
Thus the maximum volume is = 4.49243.
The larger root is TOO big and, therefore, is not the solution to the problem.
The other value, 4.49243, is the approximate solution for x.
Thus the maximum volume is
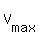 = 4.49243*(38-2*4.49243)*(22-2*4.49243) = 1696.504 cm^3 = 1697 cm^3,
rounded to the closest integer value, in cm^3. ANSWER = 4.49243*(38-2*4.49243)*(22-2*4.49243) = 1696.504 cm^3 = 1697 cm^3,
rounded to the closest integer value, in cm^3. ANSWER
Solved.
|
|
|
| |