|
Question 1166024: Find the volumes of the solids generated by revolving the regions bounded by the graphs about the given lines: y=sqrtx, y=0, x=3, and x=9 about the x=axis, the y-axis, the line at x=3, and the line at x=9. Use integration and washer/disk method. I have already solved about the x-axis to be 9/2 pi.
Found 3 solutions by CPhill, ikleyn, n2:
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! That's great that you've already solved the volume about the x-axis! Let's complete the remaining volume calculations using the disk/washer method for rotations about the $y$-axis and the vertical lines $x=3$ and $x=9$.
The region $R$ is bounded by:
* $y = \sqrt{x}$ (or $x = y^2$)
* $y = 0$ (the $x$-axis)
* $x = 3$
* $x = 9$
The region exists for $x$ from 3 to 9. The corresponding $y$ values range from $y = \sqrt{3}$ to $y = \sqrt{9} = 3$.
---
## 1. Volume about the $x$-axis
You stated you found this to be $9\pi/2$. Let's confirm using the **Disk Method** with a vertical element (integration with respect to $x$):
$$V_x = \pi \int_{3}^{9} [f(x)]^2 dx$$
$$V_x = \pi \int_{3}^{9} (\sqrt{x})^2 dx$$
$$V_x = \pi \int_{3}^{9} x dx$$
$$V_x = \pi \left[ \frac{x^2}{2} \right]_{3}^{9}$$
$$V_x = \pi \left( \frac{9^2}{2} - \frac{3^2}{2} \right) = \pi \left( \frac{81}{2} - \frac{9}{2} \right) = \pi \left( \frac{72}{2} \right) = \mathbf{36\pi}$$
***Wait, your result of $9\pi/2$ seems incorrect. Please double-check your initial calculation. The correct volume is $36\pi$.***
---
## 2. Volume about the $y$-axis
Since the axis of revolution ($x=0$) is a vertical line, we use the **Washer Method** with a horizontal element (integration with respect to $y$). The boundaries for $y$ are $\sqrt{3}$ and $3$.
The radii are measured from the $y$-axis ($x=0$) to the vertical boundaries $x=3$ and $x=9$:
* **Outer Radius ($R$):** The distance from $x=0$ to the farthest boundary $x=9$.
$$R = 9 - 0 = 9$$
* **Inner Radius ($r$):** The distance from $x=0$ to the closest boundary $x = y^2$ (the curve).
$$r = y^2 - 0 = y^2$$
$$V_y = \pi \int_{\sqrt{3}}^{3} \left(R^2 - r^2\right) dy$$
$$V_y = \pi \int_{\sqrt{3}}^{3} \left(9^2 - (y^2)^2\right) dy$$
$$V_y = \pi \int_{\sqrt{3}}^{3} (81 - y^4) dy$$
$$V_y = \pi \left[ 81y - \frac{y^5}{5} \right]_{\sqrt{3}}^{3}$$
$$V_y = \pi \left[ \left( 81(3) - \frac{3^5}{5} \right) - \left( 81(\sqrt{3}) - \frac{(\sqrt{3})^5}{5} \right) \right]$$
$$V_y = \pi \left[ \left( 243 - \frac{243}{5} \right) - \left( 81\sqrt{3} - \frac{9\sqrt{3}}{5} \right) \right]$$
$$V_y = \pi \left[ \left( \frac{1215 - 243}{5} \right) - \left( \frac{405\sqrt{3} - 9\sqrt{3}}{5} \right) \right]$$
$$V_y = \pi \left[ \frac{972}{5} - \frac{396\sqrt{3}}{5} \right]$$
$$V_y = \mathbf{\frac{972\pi}{5} - \frac{396\pi\sqrt{3}}{5} \text{ units}^3}$$
---
## 3. Volume about the line $x=3$
Since the axis of revolution ($x=3$) is a vertical line, we integrate with respect to $y$ using the **Washer Method**.
The radii are measured from $x=3$ to the outer boundary $x=9$ and the inner boundary $x=y^2$:
* **Outer Radius ($R$):** The distance from $x=3$ to $x=9$.
$$R = 9 - 3 = 6$$
* **Inner Radius ($r$):** The distance from $x=3$ to the curve $x = y^2$.
$$r = y^2 - 3$$
*Note: The integration limits remain $y=\sqrt{3}$ to $y=3$.*
$$V_{x=3} = \pi \int_{\sqrt{3}}^{3} \left(R^2 - r^2\right) dy$$
$$V_{x=3} = \pi \int_{\sqrt{3}}^{3} \left(6^2 - (y^2 - 3)^2\right) dy$$
$$V_{x=3} = \pi \int_{\sqrt{3}}^{3} \left(36 - (y^4 - 6y^2 + 9)\right) dy$$
$$V_{x=3} = \pi \int_{\sqrt{3}}^{3} (-y^4 + 6y^2 + 27) dy$$
$$V_{x=3} = \pi \left[ -\frac{y^5}{5} + \frac{6y^3}{3} + 27y \right]_{\sqrt{3}}^{3} = \pi \left[ -\frac{y^5}{5} + 2y^3 + 27y \right]_{\sqrt{3}}^{3}$$
$$V_{x=3} = \pi \left[ \left( -\frac{3^5}{5} + 2(3^3) + 27(3) \right) - \left( -\frac{(\sqrt{3})^5}{5} + 2(\sqrt{3})^3 + 27\sqrt{3} \right) \right]$$
$$V_{x=3} = \pi \left[ \left( -\frac{243}{5} + 54 + 81 \right) - \left( -\frac{9\sqrt{3}}{5} + 6\sqrt{3} + 27\sqrt{3} \right) \right]$$
$$V_{x=3} = \pi \left[ \left( 135 - \frac{243}{5} \right) - \left( 33\sqrt{3} - \frac{9\sqrt{3}}{5} \right) \right]$$
$$V_{x=3} = \pi \left[ \left( \frac{675 - 243}{5} \right) - \left( \frac{165\sqrt{3} - 9\sqrt{3}}{5} \right) \right]$$
$$V_{x=3} = \pi \left[ \frac{432}{5} - \frac{156\sqrt{3}}{5} \right]$$
$$V_{x=3} = \mathbf{\frac{432\pi}{5} - \frac{156\pi\sqrt{3}}{5} \text{ units}^3}$$
---
## 4. Volume about the line $x=9$
Since the axis of revolution ($x=9$) is a vertical line, we integrate with respect to $y$ using the **Washer Method**.
The radii are measured from $x=9$ to the inner boundary $x=3$ and the outer boundary $x=y^2$:
* **Outer Radius ($R$):** The distance from $x=9$ to the curve $x=y^2$.
$$R = 9 - y^2$$
* **Inner Radius ($r$):** The distance from $x=9$ to $x=3$.
$$r = 9 - 3 = 6$$
*Note: The integration limits remain $y=\sqrt{3}$ to $y=3$.*
$$V_{x=9} = \pi \int_{\sqrt{3}}^{3} \left(R^2 - r^2\right) dy$$
$$V_{x=9} = \pi \int_{\sqrt{3}}^{3} \left((9 - y^2)^2 - 6^2\right) dy$$
$$V_{x=9} = \pi \int_{\sqrt{3}}^{3} \left((81 - 18y^2 + y^4) - 36\right) dy$$
$$V_{x=9} = \pi \int_{\sqrt{3}}^{3} (y^4 - 18y^2 + 45) dy$$
$$V_{x=9} = \pi \left[ \frac{y^5}{5} - \frac{18y^3}{3} + 45y \right]_{\sqrt{3}}^{3} = \pi \left[ \frac{y^5}{5} - 6y^3 + 45y \right]_{\sqrt{3}}^{3}$$
$$V_{x=9} = \pi \left[ \left( \frac{3^5}{5} - 6(3^3) + 45(3) \right) - \left( \frac{(\sqrt{3})^5}{5} - 6(\sqrt{3})^3 + 45\sqrt{3} \right) \right]$$
$$V_{x=9} = \pi \left[ \left( \frac{243}{5} - 162 + 135 \right) - \left( \frac{9\sqrt{3}}{5} - 18\sqrt{3} + 45\sqrt{3} \right) \right]$$
$$V_{x=9} = \pi \left[ \left( \frac{243}{5} - 27 \right) - \left( 27\sqrt{3} + \frac{9\sqrt{3}}{5} \right) \right]$$
$$V_{x=9} = \pi \left[ \left( \frac{243 - 135}{5} \right) - \left( \frac{135\sqrt{3} + 9\sqrt{3}}{5} \right) \right]$$
$$V_{x=9} = \pi \left[ \frac{108}{5} - \frac{144\sqrt{3}}{5} \right]$$
$$V_{x=9} = \mathbf{\frac{108\pi}{5} - \frac{144\pi\sqrt{3}}{5} \text{ units}^3}$$
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the volumes of the solids generated by revolving the regions bounded by the graphs about the given lines:
y = sqrt(x), y=0, x=3, and x=9
(a) about the x=axis,
(b) about the y-axis,
(c) about the line at x=3,
(d) and about the line at x=9.
Use integration and washer/disk method. I have already solved about the x-axis to be 9/2 pi.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, part (b) is solved incorrectly.
I came to bring a correct solution for part (b).
I will use the "shell" method, which suits this problem
MUCH BETTER than the "washer/disk" method.
We can present the solid body in this case as a set of thin vertical cylindrical shells
with the axis of cylindrical shells x=0.
Each shell has the length along y-axis from y=0 to y =  , so the volume of the solid body is
V = integral over the radius 'x' from 3 to 9 of , so the volume of the solid body is
V = integral over the radius 'x' from 3 to 9 of 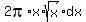 ,
Integration gives the antiderivative
F(x) = 2pi*(2/5)*x^(5/2) = (4/5)pi*x^(5/2),
and we should calculate the difference
F(9) - F(3) = (4/5)pi*(9^(5/2)-3^(5/2)) = ,
Integration gives the antiderivative
F(x) = 2pi*(2/5)*x^(5/2) = (4/5)pi*x^(5/2),
and we should calculate the difference
F(9) - F(3) = (4/5)pi*(9^(5/2)-3^(5/2)) = 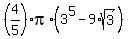 = = 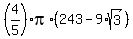 =
= =
=  = = 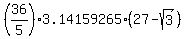 = 571.5475 cubic units, approximately. = 571.5475 cubic units, approximately.
Solved correctly.
The formula from the @CPhill solution gives the numerical value of
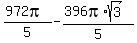 = = 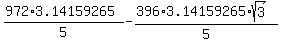 = 179.7669. = 179.7669.
which is totally wrong.
I'm somewhat surprised by the clumsiness of the instruction. It recommends
using a washer/disk method, which is ill-suited for this case.
Apparently, the instruction was written by someone with little or no knowledge of the subject.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence in solving Math problems is in the experimental stage of development
and it is far from to be a well-tuned.
It can make mistakes and produce nonsense.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
The @CPhill' solutions are copy-paste Google AI solutions (of its just old outdated version),
but there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by n2(54)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the volumes of the solids generated by revolving the regions bounded by the graphs about the given lines:
y = sqrt(x), y=0, x=3, and x=9
(a) about the x=axis,
(b) about the y-axis,
(c) about the line at x=3,
(d) and about the line at x=9.
Use integration and washer/disk method. I have already solved about the x-axis to be 9/2 pi.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, part (c) is solved incorrectly.
I came to bring a correct solution for part (c).
I will use the "shell" method, which suits this problem
MUCH BETTER than the "washer/disk" method.
We can present the solid body in this case as a set of thin vertical cylindrical shells
with the axis of cylindrical shells x=3.
In this case, each shell has the length along y-axis from y=0 to y =  and the radius (x-3),
so the volume of the solid body is
V = integral from 3 to 9 of and the radius (x-3),
so the volume of the solid body is
V = integral from 3 to 9 of  ,
Integration gives the antiderivative
F(x) = 2pi*((2/5)*x^(5/2) - 2*x^(3/2)),
and we should calculate the difference
F(9) - F(3) = [ 2pi*((2/5)*9^(5/2) - 2*9^(3/2)) ] - [ 2pi*((2/5)*3^(5/2)-2*3^(3/2)) ] =
= ,
Integration gives the antiderivative
F(x) = 2pi*((2/5)*x^(5/2) - 2*x^(3/2)),
and we should calculate the difference
F(9) - F(3) = [ 2pi*((2/5)*9^(5/2) - 2*9^(3/2)) ] - [ 2pi*((2/5)*3^(5/2)-2*3^(3/2)) ] =
= 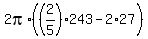 - - 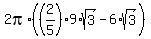 =
= =
=  = = 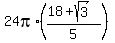 = = 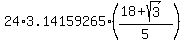 = 297.5523 approximately.
ANSWER. The volume of the solid is = 297.5523 approximately.
ANSWER. The volume of the solid is  , or about 297.5523 cubic units, approximately. , or about 297.5523 cubic units, approximately.
Solved correctly.
The formula from the @CPhill solution gives the numerical value of
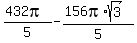 = = 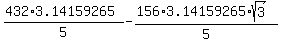 = 101.6620 = 101.6620
which is totally wrong.
I'm somewhat surprised by the clumsiness of the instruction. It recommends
using a washer/disk method, which is ill-suited for this case.
Apparently, the instruction was written by someone with little or no knowledge of the subject.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence in solving Math problems is in the experimental stage of development
and it is far from to be a well-tuned.
It can make mistakes and produce nonsense.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
The @CPhill' solutions are copy-paste Google AI solutions (of its just old outdated version),
but there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|
| |