SOLUTION: A triangular prism of cheese is measured and found to be 3 inches tall. The edges of its base are 9, 9, and 4 inches long. Several congruent prisms are to be arranged around a comm

Algebra ->  Volume -> SOLUTION: A triangular prism of cheese is measured and found to be 3 inches tall. The edges of its base are 9, 9, and 4 inches long. Several congruent prisms are to be arranged around a comm      Log On


   

Question 1163264: A triangular prism of cheese is measured and found to be 3 inches tall. The edges of its base are 9, 9, and 4 inches long. Several congruent prisms are to be arranged around a common 3-inch segment. How many prisms can be accommodated? To the nearest cubic inch, what is their total volume?
Answer by ikleyn(52790) About Me  (Show Source):
You can put this solution on YOUR website!
.

The triangle (9,9,4) is an isosceles triangle.


Let "a" be its angle opposite to the base of "4".


Then  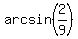sin%28a%2F2%29 = 2%2F9;  a%2F2 = arcsin%282%2F9%29 = 0.2241 radians.


Hence, the angle  "a"  is  a = 2*0.2241 = 0.4482.


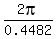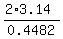The number of such angles in full angle of  2pi radians is  2pi%2F0.4482 = %282%2A3.14%29%2F0.4482 = 14.012,

or approximately 14.


Hence, the answer to the first question is 14 prisms.



Next, to find the volume of one such a prism, find first the area of its base.


To find the area of the  (9,9,4)-triangle, use the Heron's formula.


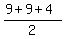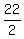Semi-perimeter is  s = %289%2B9%2B4%29%2F2 = 22%2F2 = 11;

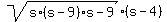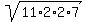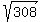hence, the area is  A = sqrt%28s%2A%28s-9%29%2As-9%29%2A%28s-4%29%29 = sqrt%2811%2A2%2A2%2A7%29 = sqrt%28308%29 = 17.55 cubic inches.


The volume of one prism = 3*17.55 = 52.65 cubic inches,

and the volume of the 14 prisms is  14*52.65 = 737 cubic inches.    ANSWER

Solved.