|
Question 1137310: Find the capacity in litres of a bucket of 24cm at the top ,16cm at the bottom and 18cm deep.Pls i need a diagram to support the solution
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
I will assume that the basket has circular section; in other word, I will assume that the basket is a part of circular cone;
this part is called "a frustum of a cone".
There are two ways to solve this problem.
One way is to apply the formula for the volume of the frustum of a cone.
If you don't know or do not remember this formula (as I myself do not remember it, for example), you can easily
find it in the Internet, searching GOOGLE with keyword "volume frustum cone".
Another way it to think a bit and to reduce this formula on your own, leaning on the knowledge about a cone volume
that you get from the school.
I will show you both ways.
Solution 1. Using the formula
This way is shorter; therefore, I will start this way.
The formula for the volume of the frusrum of a cone is
 = 
where R is the radius of the larger base; r is the radius of the shorter base and h is the frustum height.
See this Internet site
http://jwilson.coe.uga.edu/emt725/frustum/frustum.cone.html
where you will find the diagram of a frustum, too.
Now substitute the given data R = 24/2 = 12 cm, r = 16/2 = 8 cm and h = 18 cm into the formula
= =  .
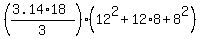and calculate.
The other way requires more explanations and more writing from me.
Solution 2
Each and every frustum of a cone is a part of some cone.
In particular, the given basket is a part of some cone.
What cone is it, in your case ?
Imagine that you increased the height from 18 to 36 centimeters, remaining the base size of 24 cm unchangeable.
Then, obviously, the smaller base will be 8 cm in diameter.
Imagine that you increased the height for another 18 cm, from 36 to 54 centimeters, remaining the base size of 24 cm unchangeable.
Then, obviously, you will get the full cone (!).
Thus, the full cone has the height of 54 centimeters and the base diameter of 24 cm.
Your basket is what will remain from this cone, when you cut the upper part by the plane parallel to its base
at the distance of 18 cm from the base.
It gives you the formula for the frustum volume
= V(large cone) - V(small cone to cut) =
=  -  =  .
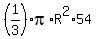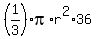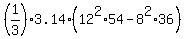Again, use your calculator.
I just completed my explanations.
I hope that after calculating the answers from both solutions, you will compare the results.
I also hope that these results will be the same.
Finally, I hope that when you complete this assignment, you will post your "Thanks" to me.
|
|
|
| |
