|
Question 1125543: The volume of ice-cream in the cone is half the volume of the cone. The cone has a 3 cm radius and height of 14 cm. What is the depth of the ice-cream, correct to 2 decimal places?
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From fig:
r/h = 3/14
r=3h/14
Volume of cone = 1/3 * pi*r^2*h
Plug values r=3 and h=14
V=132 in^3
Icecream is half volume of cone
V ice cream =66 in^3
r= 3h/14
substitute in cone volume formula
66= (1/3)*(22/7)*(3h/14)^2*h
198*7/22 = (9h^2/196)*h
63= (9h^2/196)*h
63*196/9 = h^3
7*196=h^3
h=11.11 cm height/depth of ice cream
 . .
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The volume of ice-cream in the cone is half the volume of the cone.
The cone has a 3 cm radius and height of 14 cm. What is the depth of
the ice-cream, correct to 2 decimal places?
~~~~~~~~~~~~~~~~~~~
In this problem, there is no need to calculate volumes of the cones.
The cone volumes ratio is 2 (the greater to the smaller);
hence, from similarity of the cones, the ratio of heights (greater to smaller) is 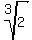 = 1.26 (rounded).
So, the depth of the ice-cream is = 1.26 (rounded).
So, the depth of the ice-cream is 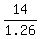 = 11.11 cm. ANSWER = 11.11 cm. ANSWER
Solved, as simple and in a way as it should be done.
---------------
By the way, the given radius of the greater cone of 3 cm is irrelevant.
This value is excessive, is not necessary, and the problem can be solved without it . . .
The answer to the question does not depend on the radius of the greater cone
and is the same for any other value of the radius of the greater cone.
|
|
|
| |