SOLUTION: A right angled triangle of which the sides are 5 and 12 in length, is made to turn round the hypotenuse.Find the volume of the double cone thus formed.

We draw the right triangle ABC slanted so that its 
hypotenuse AB is vertical.  We draw CD perpendicular 
to the hypotenuse AB.

There will be two cones, a tall one above, and a short
one below, with a common circular base.  The radius of
both cones will be the green line segment CD.  The
height of the upper cone will be AD and the height of
the lower cone will be BD.

        

The formula for the volume of a cone is .
So we will need CD, which is the radius of the base
of both cones, the height AD of the upper cone, and the height
BD of the lower cone.









ΔADC ∽ ΔACD because they are both right triangles 
which share ∠A.  So we can set up proportions:




 = the height of the upper cone.




 = the height of the lower cone.




 = the radius of the base of both cones.

The volume of the upper cone:



That simplifies to


The volume of the lower cone:



That simplifies to


Add them together:





That reduces to



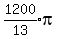Edwin