SOLUTION: Let the plane V be defined by ax + by + cz + d = 0. Which is true? A) the vector ⟨a,b,c⟩ is perpendicular to V B) the distance between V and the origin is {{{

ax + by + cz + d = 0

Let's find two points in the plane V.

Let y = 0 and z = 0

ax + b(0) + c(0) + d = 0

              ax + d = 0
                   
                  ax =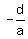 

So (-d/a,0,0) is one point in the plane V

Let x = 0 and z = 0

a(0) + by + c(0) + d = 0

              by + d = 0
                   
                  by = 

So (0,,0) is another point in the plane V

The vector between these two points is

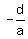⟨0-(),-0,0-0⟩  =  ⟨,,0⟩

This vector ⟨,,0⟩ is parallel to the plane V.

Let's find the dot product of it with ⟨a,b,c⟩

⟨,,0⟩•⟨a,b,c⟩ = ()a + ()b + 0(c) = d-d+0 = 0

Since that dot product is 0, the vector ⟨a,b,c⟩ is perpendicular
to to a vector parallel to the plane V and therefore is perpendicular
to the plane V.

Therefore ⟨a,b,c⟩ is normal to the plane V since its dot product
with a vector parallel to the plane V is 0.

The correct choice is A)

Edwin