Question 345483: Hi there, Please could you help with this:
find the equation of the line that contains points (3,-2, 1) and (1, 1,-3).
Thankyou muchly
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!
We find a vector parallel to the line by the method of
"subtracting the coordinates" of (3,-2, 1) and (1, 1,-3).
(1-3)i + (1-(-2))j + (-3-1)k = -2i + 3j - 4k = < -2, 3, -4 >
A parametric form of the line is then
x = 3 + (-2)t, y = -2 + 3t, z = 1 + t
Since the direction vector < -2, 3, -4 > has no 0 coordinates,
we can write an equation in symmetric form:
   
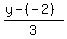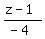Notice that I said "a" parametric or symmetric form, not "the" parametric
of symmetric form, because neither form is unique.
Edwin
|
|
|
