SOLUTION: A ladder AB rests against a vertical wall 0A. The foot 'B' of the ladder is pulled away with constant speed V a) show that the midpoint of the ladder describes the arc of a circle

Let A= (0,y) be the upper endpoint of the ladder and 
let B= (x,0) be its lover end point in coordinate plane with the origin at (0,0).


Then x^2 + y^2 = the square of the ladder length d = constant value .


The coordinates of the middle point of the ladder is  (x/2,y/2).


Since x^2 + y^2 = const, we have 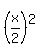  + 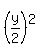 = 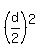, which is also a constant value.


It means that the midpoint of the ladder lies and moves on the circle of the radius , centered at the origin.


This statement DOES NOT DEPEND on the speed V of the ladder along the earth surface.
This speed can be non-uniform (not constant) - it does not changes the statement.