Vector A lies in the y-z plane 63° from the positive y-axis and has a magnitude 3.2.
It's in the y-z plane, means its x-component is 0.
Its y-component is 3.2cos(63o)
Its z-component is 3.2sin(63o)
Its components are < 0, 3.2cos(63o), 3.2sin(63o) >
or in i,j,k form
0i + 3.2cos(63o)j + 3.2sin(63ok
or just 3.2cos(63o)j + 3.2sin(63ok
as in this form it is unnecessary to write a 0 component.
Vector B lies in the x-z plane 48° from the x-axis and has a magnitude 1.4.
Find A.B, AxB and the angle between A and B
It's in the x-z plane, means its y-component is 0.
Its x-component is 1.4cos(48o) = 0.9367828489
Its z-component is 1.4sin(48o) = 1.040402756
Its components are < 0, 1.4cos(48o), 1.4sin(48o) >
1.4cos(48o)i + 0j + 1.4sin(48o)k
or just 1.4cos(48o)i + 1.4sin(48o)k
as in this form it is unnecessary to write a 0 component.
To find 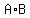 , the dot product, which is the scalar product, is
a plain old number, not a vector!
, the dot product, which is the scalar product, is
a plain old number, not a vector!
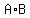

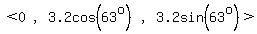

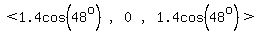



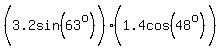 To find A x B. Work out this determinant, which will come out
in i,j,k form. This is the cross-product, or the vector-product. Unlike
the dot product, which is plain old number, the vector-product is a vector.
To find A x B. Work out this determinant, which will come out
in i,j,k form. This is the cross-product, or the vector-product. Unlike
the dot product, which is plain old number, the vector-product is a vector.

 Edwin
Edwin