Question 1184825: Object P moves according to r=(5i,-1j,2k)+t(-1,-3,1), and the object q moves according to r=(-4,-3,4)+t(1,-2,2). The distance units are meters, and t>0 is the time in seconds.
(a) Find the initial distance between the objects.
(b)Find the shortest distance between the objects, and the time when it occurs
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I understand that the coordinates of P (in meters) are
 , ,  , ,  , ,
and the coordinates of Q (in meters) are
 , ,  , ,  , with , with  in seconds. in seconds.
The square of the distance between the two objects is






That equation shows that the initial distance between the objects (in meters) is  , or approximately , or approximately  . .
With some more algebraic manipulation, we get


That last equation shows that the maximum for  , and for , and for  occurs when occurs when  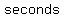 . .
At that time,
 and and   or approximately or approximately 
|
|
|