Question 1159988: Two forces act on an object at 30° to each other. One force has a magnitude of 180 N, and the resultant has a magnitude of 320 N.
a) Draw a vector diagram illustrating this situation.
b) Determine the magnitude of the second force and the direction it makes with the resultant.
c) What is the magnitude of the equilibrant force and what angle does it make with the 180N
force
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The magnitude of the resultant of the twp forces, in Newton, is  .The magnitude of a known first force, in Newton, is .The magnitude of a known first force, in Newton, is  . .
Let the magnitude of the second force be 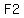 Newton. Newton.
I would draw my vector diagram as shown below.

Depending on instructor preferences, the diagram expected could have
both vectors starting from the same point with parallel segments added forming a parallelogram, like this:
 . .
I could solve it several different ways,
but here is a simple way, assuming knowing only a little trigonometry.
We are concerned with two right triangles,  and and  below. below.

 (the magnitude of R) (the magnitude of R)
 (the magnitude of F1) (the magnitude of F1)
We want to find  (the magnitude of F2). (the magnitude of F2).
From trigonometry, we find that
 and and  . .
We can find  simply using the Pythagorean theorem as simply using the Pythagorean theorem as
In physics class you could say those are the magnitudes of the horizontal and vertical components of F1.

You could say that  and and  , ,
we find the magnitude of the second force, F2, as
 . .
WE can find the measure of the angle  , ,
between 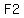 and and  from from
 , ,
which gives us 
|
|
|