|
This Lesson (Using vectors to solve problems in Mechanics: Velocity) was created by by ikleyn(53426)   : View Source, ShowAbout ikleyn:
Using vectors to solve problems in Mechanics: Velocity
Problem 1
A rowboat moves across the river. A rower in the boat heads a direction
perpendicular to the river's banks (Figure 1a). The boat's speed in this
direction is 2 m/s. The river current speed is 1 m/s.
Draw the vector of the full velocity of the boat relative to the river's bank.
You can assume that the river's banks are parallel straight lines.
Solution
The full vector of the boat velocity relative the river's banks has two components.
From one side, the boat moves across the river with oars having the velocity
component 2 m/s perpendicular to the river's banks due to rowing.
From the other side, the boat moves along the river having the velocity component
1 m/s in this direction relative to the river banks due to current.
|

Figure 1a. The river, the current
and the rowboat crossing the river
|

Figure 1b. The full vector of the
boat velocity relative to the river banks
|
The Figure 1b represents the full vector of the boat velocity relative to the river's banks. It has the component 2 m/s in the direction perpendicular to the banks and the component 1 m/s in the direction along to the river. The angle  of the Figure 1b is of the Figure 1b is  = =  , so , so  = = 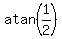 = 0.4636 rad = 26.65°. = 0.4636 rad = 26.65°.
The full speed (the magnitude of the velocity relative to the river banks) is 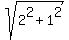 = = 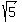 = 2.236 m/s. = 2.236 m/s.
Answer. The full vector of the boat velocity has the components 2 m/s in the direction perpendicular to the river bank, and 1 m/s in the direction along the current. This vector makes the angle 26.65° with the straight line perpendicular to the river banks. The magnitude of this vector (the full speed of the boat relative to the river banks) is 2.236 m/s.
Problem 2
A river whose width is 200 m, has the current speed of 1 m/s.
A rowboat is crossing the river. A rower heads due a direction perpendicular
to the river's banks rowing at the speed of 2 m/s relative to the water.
At what distance the rowboat will get the other bank counting downstream
from the point O opposed to the starting point D (Figure 2a)?
You can assume that the river's banks are parallel straight lines.
Solution
The rowboat has the speed of 2 m/s in the direction perpendicular to the banks
due to rowing. Hence, it will take 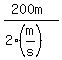 = 100 seconds to cross the river = 100 seconds to cross the river
and to get the opposite bank.
|

Figure 2a. The river, the current
and the rowboat crossing the river
|

Figure 2b. The full vector of the
boat velocity relative to the river banks
|
In 100 seconds the boat will drift downstream with the current a distance of 1  * 100 s = 100 m. * 100 s = 100 m.
Answer. The rowboat will get the other bank in 100 m downstream from the point O opposed to the starting point.
The Figure 2b (the same as the Figure 1b) represents the full vector of the boat velocity relative to the river's banks. It has the component 2 m/s in the direction perpendicular to the banks and the component 1 m/s in the direction along to the river. The angle  of the Figure 2b is of the Figure 2b is  = =  , so , so  = = 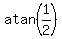 = 0.4636 rad = 26.65°. = 0.4636 rad = 26.65°.
Problem 3
A man is going to cross the river in a rowboat. The river's width is 200 m,
the current speed is of 1 m/s.
A man can row at the speed of 1 m/s relative to the water.
At what direction should the rower head the rowboat to get the other bank
at the point A directly opposed to the starting point D (Figure 3a)?
You can assume that the river's banks are parallel straight lines.
Solution
Because the boat is moving partly with the current, the boat headed due
the perpendicular to the river's banks will drift with the current. To
compensate for this cross-flow, the boat must be headed due some angle
against the current as it is shown in the Figures 3a and 3b.
|

Figure 3a. The rowboat crosses
the river overcoming the current
|

Figure 3b. The vectors of the
velocities
|
The velocity of the rowboat relative to the banks Vrb will be the sum of the velocity of the rowboat relative to the water Vrw and the velocity of the current relative to the river's banks Vcb: Vrb = Vrw + Vcb.
The magnitudes of the velocities |Vrw| and |Vcb| are |Vrw| = 2 m/s and |Vcb| = 1 m/s.
From the right triangle of the Figure 3b we have for the angle  : :  = = 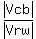 = =  . Hence, . Hence,  = = 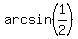 = 30°. = 30°.
From the same right triangle of the Figure 3b we have for the velocity magnitude |Vrb|: |Vrb| = 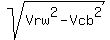 = = 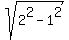 = = 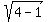 = =  =~ 1.732 m/s. =~ 1.732 m/s.
Answer. The rower must head the rowboat due the direction that makes the angle 30° with the perpendicular to the river's banks to get the other bank at the point directly opposed to the starting point. Under the given conditions, the rowboat speed perpendicular the the river's banks will be 1.732 m/s. It will takes 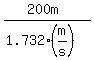 = 115.5 seconds for the rowboat to cross the river. = 115.5 seconds for the rowboat to cross the river.
Problem 4
In rainy weather the drivers who drive their cars on the highway, can see the slanting
raindrops behind the car's side windows (Figure 4a).
Calculate the angle that the raindrops makes with the vertical (Figure 4b) as
viewed by the driver, if the raindrop speed near the earth surface is 10 m/s
(meters per second) and the car's speed is 65 mph (miles per hour).
Assume that raindrops fall vertically down in the coordinate system connected
to the earth.
Solution
First, let us convert the speed of 65 mph to meters per second.
1 mile = 1609 m (approximately), so 65 mph = 1609*65/3600 = 29.05 m/s.
|

Figure 4a. The slanting raindrops
behind the car's side window
|

Figure 4b. The angle between
the raindrops and the vertical
|
Relative to the moving car the falling raindrop has the horizontal velocity 29.05 m/s in the direction opposite to the car move. It has the vertical velocity of 10 m/s, too. So, the velocity of the falling raindrop relative to the car is the vector with the horizontal component 29.05 m/s and the vertical component 10 m/s. Hence, we have for the angle  with the vertical (Figure 4b) with the vertical (Figure 4b)  = = 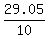 = = 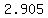 and and  = = 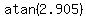 = 1.239 rad = 71°. = 1.239 rad = 71°.
Answer. The angle that the raindrops makes with the vertical as viewed by the driver is 71°.
This lesson has been accessed 8355 times.
|
| |

