|
This Lesson (Using vectors to solve problems in Mechanics: Force) was created by by ikleyn(52786)   : View Source, ShowAbout ikleyn:
Using vectors to solve problems in Mechanics: Force
Problem 1
A 100-pound box is pulled at a constant speed on a horizontal surface by the force parallel to
the floor (Figure 1). The friction coefficient is  = 0.2. = 0.2.
Find the magnitude of the applied force.
Solution
At the given conditions, the friction force has the magnitude F_frict =  * Weight = 0.2*100 = 20 pounds. * Weight = 0.2*100 = 20 pounds.
So, the applied force should have the same magnitudes as the friction force, i.e. 20 pounds providing
the uniform move of the box.
Answer. The magnitude of the applied force is equal to 20 pounds.
|

Figure 1. The body on the horizontal floor
|
Problem 2
A 100-pound box is pulled at a constant speed on a horizontal floor by the force of 20.7 pounds
that makes an angle  = 30° with the horizontal (Figure 2). Find the friction coefficient. = 30° with the horizontal (Figure 2). Find the friction coefficient.
Solution
Decompose the given force F into the horizontal and vertical components.
The horizontal component is equal to |F|*cos(30°), the vertical component is |F|*sin(30°).
The reaction force N acts from the floor vertically up to the box. Together with
the vertical component Fy it balances the weight: |W| = Fy + |N|. So, |N| = |W| - Fy.
The friction coefficient is the ratio of the shear force Fx to the reaction force |N|:
 = = 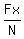 = = 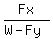 = =  = = 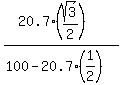 = 0.2. = 0.2.
|

Figure 2. The body on the horizontal floor
|
Answer. The friction coefficient is equal to 0.2.
Problem 3
The inclined plane makes an angle  with the horizontal as shown in Figure 3. with the horizontal as shown in Figure 3.
A 100-pound box stands at rest on the inclined plane kept by the friction force
(force of static friction) which is assumed large enough.
Find the range of the angle  values where the force of static friction is over values where the force of static friction is over
the shear force, if the static friction coefficient is  . .
Solution
The component of the weight normal to the inclined plane is  = = 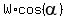 (normal force). (normal force).
The component of the weight parallel to the inclined plane is 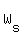 = = 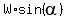 (shear force). (shear force).
The force of static friction at these conditions is 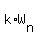 . .
|

Figure 3. The body at rest on the inclined plane
|
The condition "the force of static friction is over the shear force" is the inequality
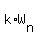 > > 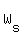 , or , or 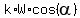 > > 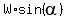 . .
It is equivalent to the inequality  < <  . .
For these angles  the force of static friction is over the shear force. the force of static friction is over the shear force.
Answer. In the range of angles  with with  < <  , the force of static friction is over the shear force. , the force of static friction is over the shear force.
Problem 4
A 100-pound box can move without friction on a 15° ramp as shown in Figure 5.
You can imagine that the box is placed on a cart and the total weight of the box and
the cart is 100 pounds.
The cart is held on the ramp surface by a string, which is tied to a peg on the top of
the ramp, so the cart and the box do not move. The string is parallel to the ramp surface.
Find the tension of the string.
Solution
This time the friction is absent, according to the condition, so we are not interested
in calculating the normal force to the inclined surface. All that we need to know is the
shear force only.
|

Figure 4. The cart at rest on the inclined
plane fixed by a string
|
The shear force is the component of the weight parallel to the inclined plane.
It is equal to 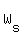 = = 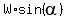 = = 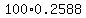 = = 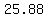 lbs. lbs.
The tension force of the string balances the shear force. Hence, the magnitude of the tension force is equal to 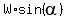 = = 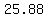 lbs. lbs.
Answer. The tension force of the string is equal to 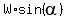 = = 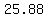 lbs. lbs.
Problem 5
The inclined plane makes an angle  with the horizontal as shown in Figure 5. with the horizontal as shown in Figure 5.
A 100-pound box is pulled up on the inclined plane by the force F parallel to its surface.
Find the magnitude of this force, if the kinematic friction coefficient  is equal to 0.2. is equal to 0.2.
Solution
The component of the weight normal to the inclined plane is  = = 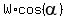 (normal force). (normal force).
The component of the weight parallel to the inclined plane is 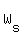 = = 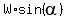 (shear force). (shear force).
The force of kinematic friction at these conditions is 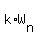 . .
|

Figure 5. The body pulled up on the inclined plane
|
The force which provides pulling up should overcome the force of kinematic friction and the component 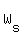 . So, its magnitude should be equal to . So, its magnitude should be equal to
|F| = 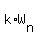 + + 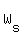 , or , or
|F| = 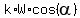 + + 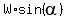 . .
For the given conditions, 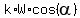 + + 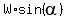 = 0.2*100*cos(15°) + 100*sin(15°) = 0.2*100*0.9659 + 100*0.2588 = 45.2 lbs. = 0.2*100*cos(15°) + 100*sin(15°) = 0.2*100*0.9659 + 100*0.2588 = 45.2 lbs.
Hence, the force magnitude |F| = 45.2 lbs.
Answer. The force that provides pulling up the box on the inclined plane has the magnitude |F| = 45.2 lbs.
This lesson has been accessed 3976 times.
|
| |

