Find an angle between 0 and 2pi that is coterminal with: (27pi)/10,
I'll only do the first two, the other two are done the same way:
To find coterminal angles we add  to the angle, where
n is some integer, positive, negative, or zero.
Therefore when we find n, the answer will be
to the angle, where
n is some integer, positive, negative, or zero.
Therefore when we find n, the answer will be 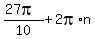 Since we want the coterminal angle to be between 0 and
Since we want the coterminal angle to be between 0 and  ,
we write an inequality which indicates that:
,
we write an inequality which indicates that:
 Divide through by
Divide through by 
 Multiply through by 10
Multiply through by 10
 Subtract 27 from all three sides:
Subtract 27 from all three sides:
 Divide through by 20
Divide through by 20

 There is only one integer between -1.35 and -0.35, namely -1.
So n = -1, therefore the answer is
There is only one integer between -1.35 and -0.35, namely -1.
So n = -1, therefore the answer is
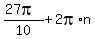


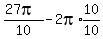
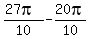
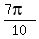 ----------------------
----------------------
coterminal with (-pi)/6,
Same way:
We add  and the answer will be
and the answer will be 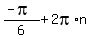 , when we find n.
Since we want the coterminal angle to be between 0 and
, when we find n.
Since we want the coterminal angle to be between 0 and  ,
we write the inequality which indicates that:
,
we write the inequality which indicates that:
 Divide through by
Divide through by 
 Multiply through by 6
Multiply through by 6
 Add 1 to all three sides:
Add 1 to all three sides:
 Divide through by 12
Divide through by 12

 There is only one integer between
There is only one integer between  and
and 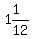 , namely 1.
So n = 1, therefore the answer is
, namely 1.
So n = 1, therefore the answer is

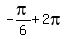
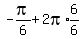
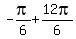
 ---------------------
Edwin
---------------------
Edwin