Question 889256: The graph of tan(T) is shifted right 45° and has the period increased to 540°. What is the
transformed equation?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your original equation is:
y = tan(x)
the equation you are looking for is:
y = tan((2/3)*(x-45))
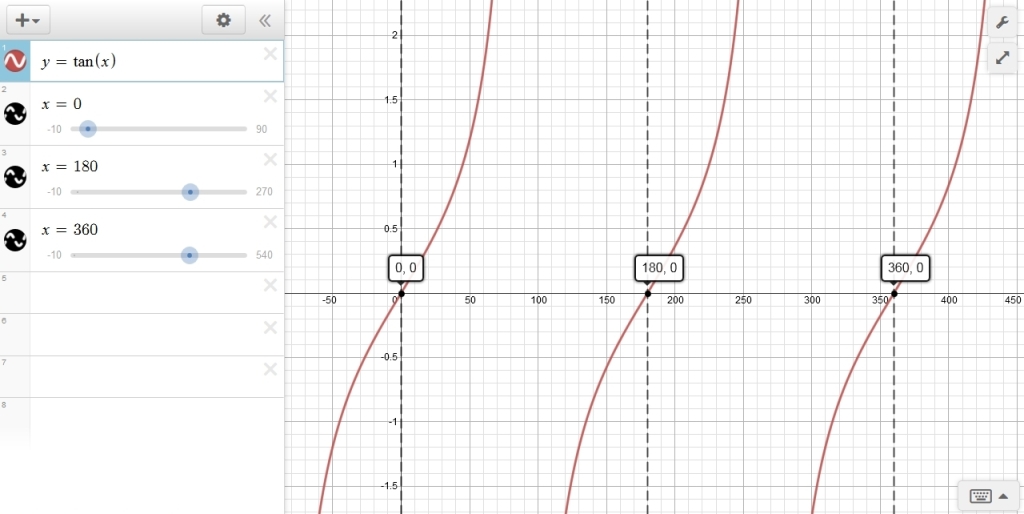
here's a graph of your original equation:
the period is 360 degrees from 0 degrees to 360 degrees.
the tangent function passes through the zero mark 3 times during the period at the zero degree mark, the 180 degree mark, and the 360 degree mark.
the end of each period is the beginning of the next period.
here's a graph of your revised equation with a shift to the right of 45 degrees only.
the period has shifted to the right 45 degrees.
instead of going from 0 to 360, it is going from 45 to 405.

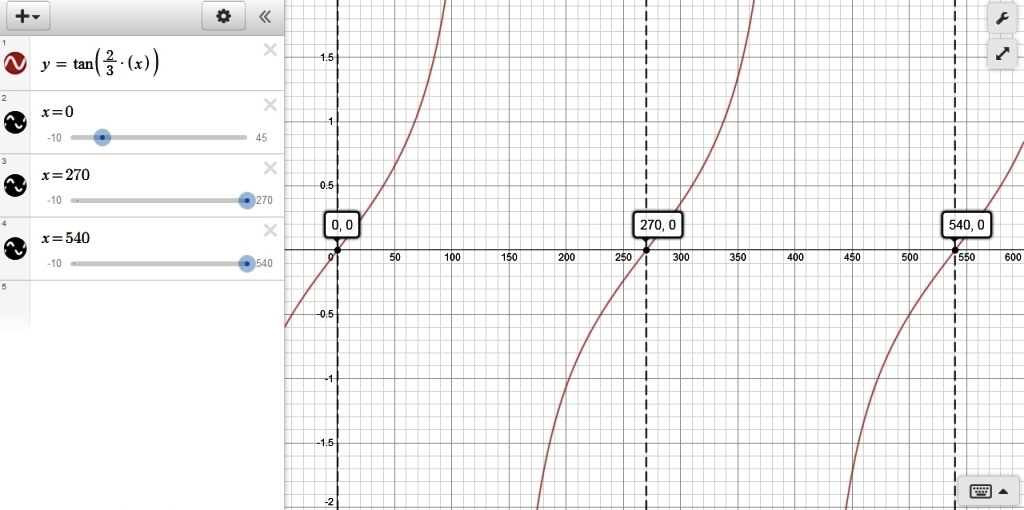
here's a graph of your revised equation with a period of 540 degrees only.
the shift of 45 degrees to the right is not included in this graph.
while the original period was 360 degrees from 0 to 360, the period is now 540 degrees from 0 to 540.
the tangent function goes through the zero point the same three times, only it is now at the 0 degree mark and the 270 degree mark and the 540 degree mark.
here's a graph of your revised equation with a period of 540 degrees and a shift of 45 degrees to the right.
the period how now shifter from starting at 0 degrees and ending at 540 degrees to starting at 45 degrees and ending at 585 degrees.
this changes the zero crossing from 0, 270, 540 to 45, 315, 585.

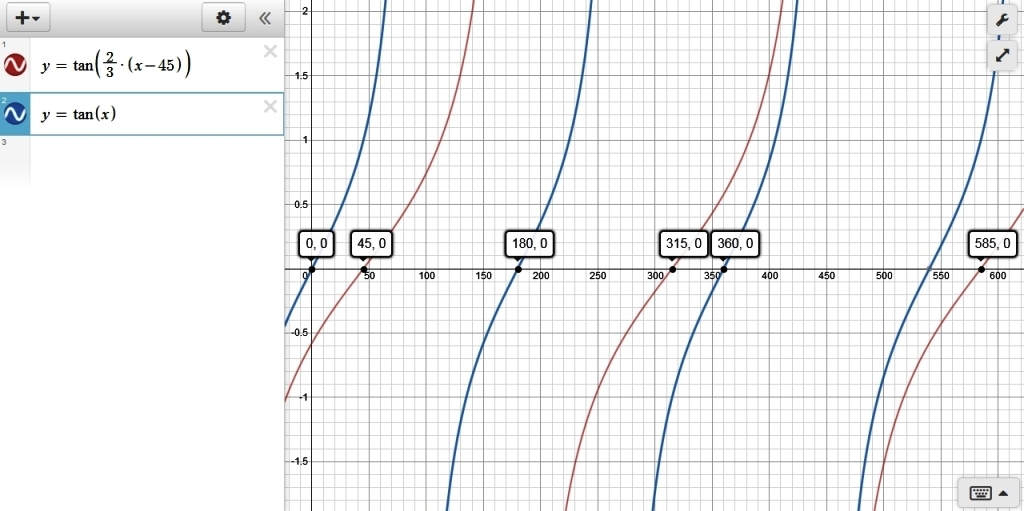
here's a graph of both your original equation and your revised equation.
the original equation is shown in blue.
it starts at 0 degrees and ends at 360 degrees and has zero crossing at 0, 180, and 360 degrees.
the blue line that crosses the zero at 540 degrees is part of the next cycle which started at 360 degrees and has zero crossings at 360, 540, and 720 degrees.
disregard that fourth blue line.
the problem with repeating functions is that you can't just show one cycle of them. they repeat endlessly.
the first 3 blue lines belong to the original function through one cycle of it.
that fourth blue line belongs to the next cycle.
the revised equation is shown in red.
it starts at 45 degrees and goes through the zero crossing at 45 degrees and 315 degrees and 585 degrees.
its period is 540 degrees from 45 degrees to 585 degrees.
|
|
|