Hi, there--
The Problem:
find (1+isqrt3)^8
Solution:
You can multiply out 8 factors of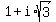 
using the distributive property. For example,
Expanded out it looks like this.
Now simplify by combining like terms.
We would repeat this process until we had raised 1+i*sqrt(3) to the 8th power.
Another method, is to use the Binomial Theorem to determine the coefficients of each term when we
raise an expression to the 8th power. I'll show this solution because it's worth knowing how to do.
If you prefer the "multiply it out" solution, email me and I'll get it to you.
There is a very nice explanation of the Binomial Theorem here:
http://www.regentsprep.org/Regents/math/algtrig/ATP4/bintheorem.htm
In short, we use combinations to find the coefficients of each terms. So for (a+b)^8 we get
(a+b)^8 = 8C0*a^8b^0 + 8C1*a^7b^1 + 8C2a^6b^2 + 8C3*a^5b^3 + 8C4*a^4b^4 + 8C5a^3b^5 +
8C6*a^2b^6 +8C7a^1b^7 + 8C8a^0b^8
This looks messy and complicates at first be as you look you can see many patterns in the way the
equation is constructed.
Let's calculate the combinations:
8C0=1
8C1=8
8C2=28
8C3=56
8C4=70
8C5=56
8C6=28
8C7=8
8C8=1
Substitute these into the equation. Also, simplify a^0=b^0=1 and a^1=a and b^1=b.
Now we can use this formula with your polynomial expansion.
Let a = 1 and
Let b = i*sqrt(3)
Substitute these into the binomial expansion.
Now start simplifying. 1 raised to any power is 1, so we can immediately simplify there.
Notice the pattern when we raise the complex number i to a power:
i^0 = 1
i^1 = i
i^2 = -1
i^3 = -i
i^4 = 1
i^5 = i
i^6 = -1
i^7 = -i
i^8 = 1
Simplify the polynomial expansion using these values.
Lastly, we simplify the radical(3) terms.
Now, combine like terms.
This may seem complicated at first, but it is far fewer calculations that repeatedly using the distributive
property. I hope this helps. If you have any questions about this, or would like to see the distributive
property method, please feel free to email.
Mrs Figgy
math.in.the.vortex@gmail.com
