SOLUTION: The question can be viewed here: https://drive.google.com/file/d/0B7JzYDUirqMKNEU1WW8yM0Q3Nlk/edit?usp=sharing Thanks!!

Algebra ->  Trigonometry-basics -> SOLUTION: The question can be viewed here: https://drive.google.com/file/d/0B7JzYDUirqMKNEU1WW8yM0Q3Nlk/edit?usp=sharing Thanks!!       Log On


   

Question 827006: The question can be viewed here:
https://drive.google.com/file/d/0B7JzYDUirqMKNEU1WW8yM0Q3Nlk/edit?usp=sharing
Thanks!!
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20065) About Me  (Show Source):
You can put this solution on YOUR website!
Your solution is below:
Edwin

Answer by AnlytcPhil(1810) About Me  (Show Source):
You can put this solution on YOUR website!
Question 827006
AP, PQ and QR are three equal line segments inclined at angles
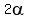alpha,2alpha, and3alpha respectively to line
segment AB.  Show that

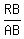tan(< BAR) = RB%2FAB = 




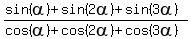
Draw PS and QT perpendicular to AB, PU and QV parallel to AB.


PS%2FAP=sin%28alpha%29

PS=AP%2Asin%28alpha%29

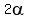< QPU = 2alpha  Parallel lines cut by transversal

QU%2FPQ=sin%28QPU%29=sin%282alpha%29

QU=PQ%2Asin%282alpha%29

QT=QU%2BUT=QU%2BPS=PQ%2Asin%282alpha%29%2BAP%2Asin%28alpha%29

RV%2FQR=sin%283alpha%29

RV=QR%2Asin%283alpha%29

RB+=+RV%2BVB+=+RV%2BQT+=+QR%2Asin%283alpha%29%2BPQ%2Asin%282alpha%29%2BAP%2Asin%28alpha%29

Since we are given AP=PQ=QR

RB=AP%2Asin%28alpha%29%2BAP%2Asin%282alpha%29%2BAP%2Asin%283alpha%29

RB=AP%28sin%28alpha%29%2Bsin%282alpha%29%2Bsin%283alpha%29%29
---------------------------------------

Exactly similar to above using cosines instead of sines and

AS, PU and QV instead of PSQU and RV, you can prove

RB=AP%28sin%28alpha%29%2Bsin%282alpha%29%2Bsin%283alpha%29%29

then 



Cancel the AP's and get

tan(BAR) = 


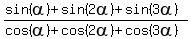  Edwin