You can
put this solution on YOUR website!
sin(θ + 4°) = cos(θ + 6°)
Use the cofunction identity cos(a) = sin{90°-a)
sin(θ + 4°) = sin[90° - (θ + 6°)]
sin(θ + 4°) = sin[90° - θ - 6°)]
sin(θ + 4°) = sin(84° - θ)
Then we use the fact that
if sin(α) = sin(β)
then one or both of these
hold
α = β + 360°n
α = (180°-β) + 360°n
for integer n
Using the first one
α = β + 360°n
θ + 4° = 84° - θ + 360°n
2θ = 80° + 360°n
θ = 40° + 180°n
letting n=0 give θ = 40°
letting n=1 give θ = 220°
Using the second one
α = 180° - β + 360°n
θ + 4° = 180° - (84 - θ) + 360°n
θ + 4° = 180° - 84° + θ + 360°n
4° = 96° + 360°n
-92° = 360°n
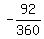 = n
= n
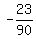 = n
That is extraneous because n is an integer.
So the only solutions between 0° and 360° are
θ = 40° and θ = 220°
and the general solution is
θ = 40° + 180°n, for any integer n.
Edwin
= n
That is extraneous because n is an integer.
So the only solutions between 0° and 360° are
θ = 40° and θ = 220°
and the general solution is
θ = 40° + 180°n, for any integer n.
Edwin