Question 812608: cos^2x-5cosx+4=0
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 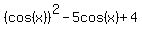 could be called a quadratic polynomial in could be called a quadratic polynomial in  . .
It has a term in  squared, a term in squared, a term in  , and an independent term. , and an independent term.
It can be factored as
 , ,
which means the equation can be re-written as
 . .
That is not easy to see, but someone saw something like that before,
and invented a trick called "change of variable".
If you make the change of variable  , ,
substituting  for for  , you get , you get

That equation is not that scary,
and you probably would solve it easily by factoring,
first re-writing it as the factored form
 , ,
and then finding that the solutions derive from
 --> --> 
and
 --> --> 
That would mean (going back to the original variable)
 , which has many solutions, , which has many solutions,
and
 , which has no solutions. , which has no solutions.
 , so , so 
works for the angle measuring  in degrees, in degrees,
which is also known as 0 radians (where radian is a ratio of length with no units).
Since angles are useful to measure turns (of a screw, or a knob, or a skater),
we can talk about angles measuring  , or , or 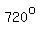
(that is 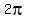 radians), radians),
or greater multiples.
When we care about the direction of the turn,
turns in one direction are counted as positive angles,
and turns in the other direction count as negative angles,
so there is an infinite number of solutions.
We could express them all with a formula.
In degrees, it would be
 where where  is any integer. is any integer.
In radians, it would be
 where where  is any integer. is any integer.
|
|
|