The other tutor gave decimals and also missed solutions. I think your teacher wanted
exact values, which as you will see are  ,
,  ,
, 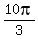 f(x) = 9 - 18cos(x+
f(x) = 9 - 18cos(x+ )
9 - 18cos(x+
)
9 - 18cos(x+ ) = 0
-18cos(x+
) = 0
-18cos(x+ ) = -9
cos(x+
) = -9
cos(x+ ) =
) =  The angles whose cosine is
The angles whose cosine is  have reference angle 60° in QI and QIV
x+
have reference angle 60° in QI and QIV
x+ =
= 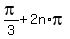 and x+
and x+ =
= 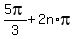 where n is an integer.
Solve the first equation:
x+
where n is an integer.
Solve the first equation:
x+ =
= 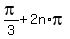 x =
x = 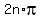 We require that solutions be on the positive x-axis
2n*pi > 0, so n = 1,2,...
Solutions for that are
We require that solutions be on the positive x-axis
2n*pi > 0, so n = 1,2,...
Solutions for that are  ,
,  ,
,  , etc.
Those are approximately 6.3, 12.6, 18.8, etc.
(I'm using decimals only to tell which are the smallest three exact
solutions, not for final answers)
Solve the second equation:
x+
, etc.
Those are approximately 6.3, 12.6, 18.8, etc.
(I'm using decimals only to tell which are the smallest three exact
solutions, not for final answers)
Solve the second equation:
x+ =
= 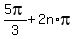 x =
x = 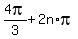 x =
x = 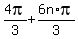 x =
x =  x =
x = 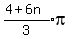 We require
We require
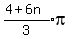 > 0
> 0
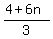 > 0
4 + 6n > 0
6n > -4
n >
> 0
4 + 6n > 0
6n > -4
n > 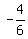 n >
n >  So n = 0, 1, 2, ...
Solutions on the positive x-axis for are
So n = 0, 1, 2, ...
Solutions on the positive x-axis for are
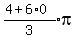 ,
, 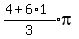 ,
, 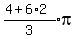 , etc.
or
, etc.
or
 ,
, 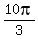 ,
, 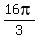 , etc.
Those are approximately 4.2, 10.5, 16.8, etc.
(I'm using decimals only to tell which are the smallest three exact
solutions)
So the smallest is the one that is approximately 4.2, which is
, etc.
Those are approximately 4.2, 10.5, 16.8, etc.
(I'm using decimals only to tell which are the smallest three exact
solutions)
So the smallest is the one that is approximately 4.2, which is  .
The next one after that is the one that is approximately 6.3 or
.
The next one after that is the one that is approximately 6.3 or  .
The next one after that is the one that is approximately 10.5 or
.
The next one after that is the one that is approximately 10.5 or 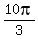 Answers:
Answers:  ,
,  ,
, 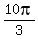 Edwin
Edwin