Question 786565: tan x + √3= 0 → tan x =−√3
The term tan x is now isolated in the equation. Find a particular solution on the interval (0, π).
x =2π/3 , 0 < x < π
On (-Infiniti, infiniti ), there are an infinite number of solutions. Write the general form of the solution. Your answer should be exact. (Use n as an integer constant. Enter your response in radians.)
x=???????????
Found 2 solutions by josmiceli, Edwin McCravy:
Answer by josmiceli(19441)   (Show Source):
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website! tan x + √3= 0 → tan x =−√3
The term tan x is now isolated in the equation. Find a particular solution on the interval (0, π).
x =2π/3 , 0 < x < π
On (-Infiniti, infiniti ), there are an infinite number of solutions. Write the general form of the solution. Your answer should be exact. (Use n as an integer constant. Enter your response in radians.)
x=???????????
Since tangent has period p, we can add any
positive, negative, or zero multiple of p to 2p/3.
Answer = 2p/3 + np.
You could get an LCD of 3, and then factor out p on top and get 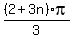 , but that is not necessary.
Edwin
|
|
|
