Question 733683: Dermont and tony are competing to see whose house is the tallest. Early in the afternoon, tony, who is 4 feet tall, measured his shadow to be 9.6 inches and the shadow of his house to be 62.4 inches. Later in the day, dermont, who is five feet all, measured his shadow to be 15.6 inches and the shadow of his house to be 62.4 inches. Who lives in the taller house?
Found 3 solutions by lynnlo, rothauserc, ikleyn:
Answer by lynnlo(4176)   (Show Source): (Show Source):
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! we use right triangle ratios to solve this problem:
The ratio (note that Tony's height in inches is 48) for Tony's house height is
48/9.6 = x/62.4, cross multiply fractions, 9.6x = 2995.2, x=312 inches or 26 feet in height
The ratio (note that Dermont's height in inches is 60) for Dermont' house is
60/15.6 = y/62.4, cross multiply fractions, 15.6y = 3744, y=240 inches or 20 feet in height
Therefore Tony's house is taller
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Dermont and tony are competing to see whose house is the tallest.
Early in the afternoon, Tony, who is 4 feet tall, measured his shadow to be 9.6 inches
and the shadow of his house to be 62.4 inches.
Later in the day, Dermont, who is five feet all, measured his shadow to be 15.6 inches
and the shadow of his house to be 62.4 inches. Who lives in the taller house?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We assume that all measurements relate to horizontal ground surface.
If so, then we write the proportion for the Tony's house height 'T'
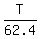 = = 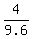 ,
which gives the Tony's house height T = ,
which gives the Tony's house height T = 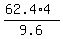 = 26 feet.
Next, we write the proportion for the Dermont's house height 'D' = 26 feet.
Next, we write the proportion for the Dermont's house height 'D'
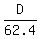 = = 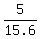 ,
which gives the Dermont's house height D = ,
which gives the Dermont's house height D = 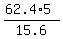 = 20 feet.
ANSWER. Tony's hous is taller. = 20 feet.
ANSWER. Tony's hous is taller.
Solved.
The solution in the post by @lynnlo is incorrect.
=======================================
The fact that measurements for the height-shadow are made at the different time of the day
does not interfere to write the proportions as they are written in my solution.
The triangles that are similar and should be similar and whose similarity is used,
remain similar at any time of measurements.
|
|
|