SOLUTION: Use an Addition or Subtraction Formula to find the exact value of the expression. sin( -5π/12)

Algebra ->  Trigonometry-basics -> SOLUTION: Use an Addition or Subtraction Formula to find the exact value of the expression. sin( -5π/12)       Log On


   

Question 667117: Use an Addition or Subtraction Formula to find the exact value of the expression.
sin( -5π/12)

Found 3 solutions by lynnlo, MathTherapy, greenestamps:
Answer by lynnlo(4176) About Me  (Show Source):
You can put this solution on YOUR website!
0.9659======OR===========-1+√3/2√2

Answer by MathTherapy(10719) About Me  (Show Source):
You can put this solution on YOUR website!
Use an Addition or Subtraction Formula to find the exact value of the expression.
sin( -5π/12)
=================
@Lynnlo's answer: 0.9659======OR===========-1+√3/2√2, is ALL WRONG!
Isn't the EXACT value needed? .9659 is certainly NOT THAT!! And, I have no idea what "-1+√3/2√2" is!!
=====================
You can use either, sin (A - B) = sin A cos B - cos A sin B (DIFFERENCE-of-2 ANGLES formula), or 
                    sin (A + B) = sin A cos B + cos A sin B (SUM-of-2 ANGLES formula)

Using sin (A - B) = sin A cos B - cos A sin B (DIFFERENCE-of-2 ANGLES formula)

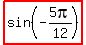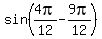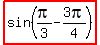highlight%28sin+%28-+5pi%2F12%29%29 = sin+%284pi%2F12+-+9pi%2F12%29 = highlight%28sin+%28pi%2F3+-+3pi%2F4%29%29

  sin (A - B) = sin A cos B - cos A sin B
, with matrix%282%2C1%2C+A+=+pi%2F3%2C+B+=+3pi%2F4%29 
 = highlight%28-+sqrt%286%29%2F4+-+sqrt%282%29%2F4%29 = highlight%28%28-+sqrt%286%29+-+sqrt%282%29%29%2F4%29
=======================================================================================
Using sin (A + B) = sin A cos B + cos A sin B (SUM-of-2 ANGLES formula)

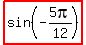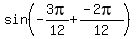highlight%28sin+%28-+5pi%2F12%29%29 = sin+%28-+3pi%2F12+%2B+%28-+2pi%29%2F12%29 = highlight%28sin+%28-+pi%2F4+%2B+%28-+pi%29%2F6%29%29

     sin (A + B) = sin A cos B + cos A sin B
, with matrix%282%2C1%2C+A+=+-+pi%2F4%2C+B+=+-+pi%2F6%29 
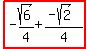 = highlight%28-+sqrt%286%29%2F4+%2B+%28-+sqrt%282%29%29%2F4%29 = highlight%28%28-+sqrt%286%29+-+sqrt%282%29%29%2F4%29

Answer by greenestamps(13295) About Me  (Show Source):
You can put this solution on YOUR website!


(1) using an angle addition formula....

-5pi%2F12=%28-3pi%2F12%29%2B%28-2pi%2F12%29=%28-pi%2F4%29%2B%28-pi%2F6%29

Use sin%28A%2BB%29=sin%28A%29cos%28B%29%2Bcos%28A%29sin%28B%29 with A=-pi%2F4 and B=-pi%2F6

sin%28-5pi%2F12%29=sin%28-pi%2F4%29cos%28-pi%2F6%29%2Bcos%28pi%2F4%29sin%28-pi%2F6%29

sin%28-5pi%2F12%29=-sqrt%286%29%2F4-sqrt%282%29%2F4%29
sin%28-5pi%2F12%29=%28-sqrt%286%29-sqrt%282%29%29%2F4

OR...

(2) using an angle subtraction formula...

-5pi%2F12=%283pi%2F12%29-%288pi%2F12%29=%28pi%2F4%29-%282pi%2F3%29

Use sin%28A-B%29=sin%28A%29cos%28B%29-cos%28A%29sin%28B%29 with A=pi%2F4 and B=2pi%2F3

sin%28-5pi%2F12%29=sin%28pi%2F4%29cos%282pi%2F3%29-cos%28pi%2F4%29sin%282pi%2F3%29

sin%28-5pi%2F12%29=-sqrt%282%29%2F4-sqrt%286%29%2F4
sin%28-5pi%2F12%29=%28-sqrt%282%29-sqrt%286%29%29%2F4

ANSWER: sin%28-5pi%2F12%29=%28-sqrt%286%29-sqrt%282%29%29%2F4