Question 634328: Tan B/2 = 15/151. I need to solve for B. I think it close to 11 degrees, but I need the exact number.
Thank you,
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Some points before we start:- Please put arguments to functions in parentheses like you see above. Without the parentheses the argument is unclear. Your equation might be
 which is a different equation with different solutions. If actually is the equation, then you will probably have to re-post your question (with the parentheses) because the solution below will not work for this. - The Trig functions are periodic. This usually means there are an infinite number of solutions to equations where the variable is an angle. Even if 11 degrees is a solution, so will other angles: 11 + 180, 11 + 360, 11 - 180, 11 -360, etc.
- The only time you can work with "exact numbers" in Trig is when you are working with special angles. When you learn Trig, you learn what these special angles are and what the various Trig ratios are for these angles. After we multiply both sides by 2 and get
 we should recognize that 30/151 is not one of the special angle values for tan. Without special angles we cannot get an "exact number" for the answer. We can only get decimal approximations.
As I mentioned above, the first step is to multiply both sides by 2 giving us:
Since 30/151 is not a special angle ratio for tan, we will reach for our calculators. First we turn the fraction into a decimal:
And then we use inverse tan button (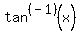
This gives us the reference angle for B, not a "one and only answer" as some mistakenly think.
Next we decide the quadrants where B must terminate. Our tan ratio, 0.19867550, is a positive number. Angles have positive tangents in the 1st and 3rd quadrants. This fact, plus the reference angle give us a way to express the solutions to your equation:
B = 11.23694426 + 360n (for the 1st quadrant)
or
B = 180 + 11.23694426 + 180 + 360n
which simplifies to:
B = 191.23694426 + 360n (for the 3rd quadrant)
Notes about the solution:- Both equations
B = 11.23694426 + 360n
B = 191.23694426 + 360n
give us (approximate) solutions to your equation. - The "+ 360n" is how we include all the co-terminal angles without having to list them individually. For example,
B = 11.23694426 + 360n
says "B is 11.23694426 degrees or any other angle that is co-terminal with 11.23694426 degrees". - To work with these equations, you replace the "n" with various integers. For each integer value for n you get a value for B that is a solution to your equation. For example, if we make "n" be -3 and use the second equation:
B = 191.23694426 + 360(-3)
B = 191.23694426 + (-1080)
B = -888.76305574
which is another solution to your equation. (Try tan(-888.76305574) and see if you get 0.19867550 (or something very close to it)). - Some textbooks/teachers use a different letter than "n", like "k". The name of the letter is not important. What is important is that it represents an integer.
- With tan equations, some clever people take advantage of the fact the the period for tan is actually 180, not 360. So we can actually use just one equation for the solution:
B = 11.23694426 + 180n - As mentioned earlier, we are working with decimal approximations since B was not a special angle. So feel free to round off (or use more decimal places) as you see fit.
|
|
|
