Question 630723: Suppose that you are on a salvage ship in the Gulf of Mexico. Your sonar system has located a sunken Spanish galleon at a slant distance of 68.3 meters from your ship, with an angle of depression of 27°52′.
a) How deep is the water at the galleon’s location?
b) How far must you sail to be directly above the galleon?
c) You sail directly toward the spot over the galleon. When you have gone 520 meters, what should the angle of depression be?
i'm stuck with c. i got b, x=603.8m, then in c it says 520m, which is smaller than 604.8cm? how is it possible? or i have wrong interpretation?
pls. help!!
Found 2 solutions by rmnavalta, jsmallt9:
Answer by rmnavalta(7)   (Show Source): (Show Source):
You can put this solution on YOUR website! I've corrected the given from 68.3 to 683meters.
For the illustration please see this (placed on my fb profile)
https://www.facebook.com/photo.php?fbid=3633779889920&set=a.1100830367765.2014805.1436862519&type=1&relevant_count=1&ref=nf
Solution:
(a) Let d = depth of water @ galleon's location
Use sine of angle of depression = opposite / hypotenuse.
sin 27°52′=d/683
d = 683sin 27°52′ ---> Multiply both sides by 683.
d = 319.24 meters --->Ans. depth of water @ galleon's location
(b) Let x = distance the ship would sail to be directly above the galleon
Use cosine of angle of depression = adjacent / hypotenuse.
cos 27°52′=d/683
x = 683cos 27°52′ ---> Multiply both sides by 683.
x = 603.8 meters --->Ans. distance the ship would sail to be directly above the galleon
(b) Let angle B = angle of depression of the galleon when the ship has gone 520 m
Use tangent of angle of depression(angle B) = opposite / adjacent.
tan (angle B) = d/x-520
tan (angle B) = 319.24/(603.8-520) ---> Solved from (a)d=319.24 and (b)x=603.8
(angle B) = arctan (319.24/83.8) ---> Get arctan of both sides.
(angle B) = 75.29° or 75°17′ ---> Ans. angle of depression of the galleon when the ship has gone 520 m
Answers;
(a) depth of water @ galleon's location = 319.24 meters
(b) distance the ship would sail to be directly above the galleon = 603.8 meters
(c) angle of depression of the galleon when the ship has gone 520 m= 75.29° or 75°17′
God bless. Email me- rmnavalta@yahoo.com
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Below is a drawing depicting what you posted, as I understood it.
"G" is the galleon
"S" is the initial position of the ship
"T" is the position of the ship after it has traveled 520 meters towards tha galleon.
"U" is the position of the ship when it is directly above the galleon.
Angle SUG is a right angle.
The length of segment SG is the slant distance of 68.3 meters.
The length of segment ST is 520 meters
The angle of depression is angle TSG. 27 degrees and 52 minutes, in (rounded) decimal form is 27.87

This is not possible, There is no way that 520, which is just part of segment SU, could be longer than SG. SG is the hypotenuse of right triangle SGU and must be the longest side. So there is something wrong with either the 68.3 or the 520 numbers.
All I can do is tell you how to take the correct numbers and find the answers. In the equations below, replace SG with whatever the correct slant distance is and replace ST with whatever the correct "after you have gone ___ meters" distance is.
Part a. Here you are looking for the length of UG. To find this use:
sin(27.87) = UG/SG (opposite over hypotenuse)
Multiply both sides by SG:
SG*sin(27.87) = UG
Part b. Here you are looking for the length of SU. To find this use:
cos(27.87) = SU/SG (adjacent over hypotenuse)
Multiply both sides by SG:
SG*cos(27.87) = SU
Part c. Here you are looking for angle UTG. For this use:
tan(UTG) = UG/(SU-ST) (Opposite over adjacent)
ST was given to you in the problem. UG is the answer you got from part a and SU is the answer you got from part b. Put these numbers in and find a decimal value for that fraction. Then use the inverse tan button 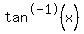 on that decimal to find the angle. on that decimal to find the angle.
|
|
|