Question 629216: For the past three years, the manager of The Toggery Shop has observed that revenue reaches a high of about $40,000 in December and a low of about $10,000 in June, and that a graph of the revenue looks like a sinusoid. If the months are numbered 1 through 36 with 1 corresponding to January, then what are the period, amplitude, and phase shift for this sinusoid? What is the vertical translation? Write a formula for the curve and find the approximate revenue for April.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! With a maximum revenue of $40000 and a minimum of $20000, halfway in between would be:
This is the vertical shift of the sinusoid.
The distance between the midway point, 25,000, and the maximum would be:
40000-25000 = 15000
This is the amplitude of the sinusoid.
From the maximum in January, month 1, to the minimum in June, month 6, is half of a full cycle. So half of a full cycle would be:
6 - 1 = 5
This makes a full cycle (IOW the period): 10.
As for the phase shift, it depends on whether you choose to use sin or cos to model. cos(x) it at its maximum when x = 0. sin(x) is halfway between the maximum and the minimum, on its way up to the maximum, when x = 0. From the information we have I think you'll agree that a) we know where the maximum is; and b) it will take some work to figure out where "halfway between the maximum and the minimum, on its way up to the maximum" occurs. So we'll go with cos.
The maximum revenue occurs at month 1. This makes the phase shift for cos: 1 to the right.
The framework for our modeling equation is something like:
y = C + A*cos(B(x - D))
If this is not exactly what you were taught then there are three explanations for the difference(s):- Letters other than A, B, C and D are used. This is not important. What is important is that there are 4 numbers which we will use and the roles they play depend only on their location in the equation, not by whatever letter happens to be used to name it.
- The letters A, B, C and D are in different places. Again this is not important. What matter is the roles the numbers play, not whether it is named A, B, C or D.
- There is no inner parentheses in the argument of cos. For reasons I cannot even begin to understand some books/teachers are teaching the equation with a form like:
y = C + A*cos(Bx-D)
This and y = C + A*cos(B(x - D)) are significantly different!
y = C + A*cos(Bx-D)
completely changes the role of B and D. To me it makes B and D much harder to understand what they are and how to work with them.
So what I'm going to do is try to explain the "good" framework equation:
y = C + A*cos(B(x - D))
in way that you could understand even if you are used to different letters or the same letters in different places. Then I will tell you how to convert the result we get into the other form:
y = C + A*cos(Bx-D)
in case you need it written that way.
- The extra term (called "C" in the framework), whether it is before the cos or after it, is the vertical shift. So we will but a 25000 in this place.
- The coefficient to cos (called "A" in the framework) is the amplitude. So we will put a 15000 in that place.
- The number in front of the inner parentheses in the argument (called "B" in the framework is not the period but it is related to the period:
 where the "p" stands for the period. In our equation we will use:
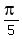 which reduces to  - The number subtracted from x in the argument (called "D" in the framework) is the phase shift. Use positive numbers for D for right shifts and use negative numbers for D for left shifts. We have a right shift of 1 so we will put a 1 in that place.
Putting all this together:
Some books/teachers put the extra term/vertical shift at the end. If so, then the equation would be:
If you have had the misfortune (my opinion) to be taught to use a form like:
y = C + A*cos(Bx-D)
then just take the answer above:
and use the Distributive Property to multiply out the argument of cos:
|
|
|
