SOLUTION: sin 4theta=8sin theta*cos^3theta-4sin theta*cos theta

Algebra ->  Trigonometry-basics -> SOLUTION: sin 4theta=8sin theta*cos^3theta-4sin theta*cos theta      Log On


   

Question 613913: sin 4theta=8sin theta*cos^3theta-4sin theta*cos theta
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
sin%284theta%29=8sin%28theta%29%2Acos%5E3%28theta%29-4sin%28theta%29%2Acos%28theta%29

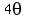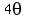On the left the only argument is 4theta. On the right the only argument is theta. So at some point we will need to change the argument of 4theta into theta. Also, the only function on the left is sin while the right has sin and cos. The left side has only one term while the right side has two. These are the kinds of things to look at when trying to prove these identities.

Changing arguments and functions is usually done with Trig. properties/identities. Changing the number of terms can be done with algebra and/or with Trig. properties/identities.

So which properties could we use on 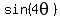sin%284theta%29? Answering this depends on:
  • A good knowledge of the various properties
  • An understanding that these properties represent patterns, that the x's, the A's and the B's in all those formulas are just place holders. If every "x" in a formula is replaced by the same number, variable or expression, then the equation is just as true as it was when it was just "x". The same can be said for the A's and B's. For example:
    cos(A+B) = cos(A)cos(B) - sin(A)sin(B)
    If we replace the A's with "q" and the B's with 10q we get:
    cos(q+10q) = cos(q)cos(10q) - sin(q)sin(10q)
  • An ability to imagine ways to rewrite what you have so it matches a pattern from one of the properties. For example, if you had cos(11q) can you see that it would be the same as cos(q+10q)? If yes, then we could use that, and the example above to transform cos(11q):
    cos(11q) = cos(q+10q) = cos(q)cos(10q) - sin(q)sin(10q)
So which properties can we use on 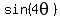sin%284theta%29? There are many possibilities, some better than others:
  • sin%284theta%29+=+sin%282%282theta%29%29
    Now we could use the sin(2x) = 2sin(x)cos(x) property:
    sin%284theta%29+=+sin%282%282theta%29%29+=+2sin%282theta%29cos%282theta%29
  • sin%284theta%29+=+sin%282theta%2B2theta%29
    Now we can use the sin(A+B) = sin(A)cos(B) + coa(A)sin(B) property:
  • sin%284theta%29+=+sin%28theta%2B3theta%29
    Now we can use the sin(A+B) = sin(A)cos(B) + coa(A)sin(B) property:
  • sin%284theta%29+=+sin%287theta-3theta%29
    Now we can use the sin(A-B) = sin(A)cos(B) - coa(A)sin(B) property:
  • sin%284theta%29+=+sin%28%281%2F2%298theta%29 on which we can use the sin%28%281%2F2%29x%29+=+0+%2B-sqrt%28%281-cos%28x%29%29%2F2%29 property:
    sin%284theta%29+=+sin%28%281%2F2%298theta%29+=+0+%2B-+sqrt%28%281-cos%288theta%29%29%2F2%29
    (Note: Algebra.com's formula software will not let me use a "plus or minua" symbol without a number (or variable) in front of it. That is why the 0's are there. They are mathematically unnecessary.)
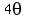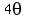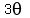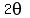One could go on forever with this. We just need to find one that looks promising. We are trying to change the argument from 4theta to theta. So the last two examples above look very unpromising because they end up with arguments that are larger that 4theta, not smaller. The first three could work. The 3rd one has an argument of 3thetawhile the first two have arguments of 2theta. To me, the first one looks simplest and easiest to work with. So we'll start with:
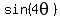
sin%284theta%29
sin%282%282theta%29%29
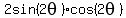
2sin%282theta%29%2Acos%282theta%29
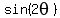We're still working our way down to arguments of just theta. It should be obvious how to deal with sin%282theta%29:
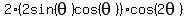
2%282sin%28theta%29cos%28theta%29%29%2Acos%282theta%29
which simplifies to:
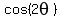4sin%28theta%29cos%28theta%29%2Acos%282theta%29
But for cos%282theta%29 there are three variations of the cos(2x) formula:
  • cos%282x%29+=+cos%5E2%28x%29+-+sin%5E2%28x%29
  • cos%282x%29+=+2cos%5E2%28x%29+-+1
  • cos%282x%29+=+1+-+2sin%5E2%28x%29
So which one do we use? Well any of them will work ultimately. But a smart choice here will make the work easier. Let's look at our expression using each of three variations of cos(2x):
4sin%28theta%29cos%28theta%29%2A%28cos%5E2%28theta%29-sin%5E2%28theta%29%29
or
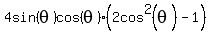
4sin%28theta%29cos%28theta%29%2A%282cos%5E2%28theta%29-1%29
or
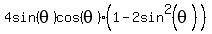
4sin%28theta%29cos%28theta%29%2A%281+-+2sin%5E2%28theta%29%29
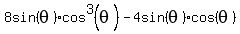All of these will work but which is best? Well the 1st and 3rd ones have sin%5E2%28theta%29 in them. Out final expression, 8sin%28theta%29%2Acos%5E3%28theta%29-4sin%28theta%29%2Acos%28theta%29 does not have any sin%5E2%28theta%29's.

So let's try the middle option:
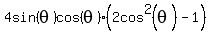
4sin%28theta%29cos%28theta%29%2A%282cos%5E2%28theta%29-1%29
We can use the Distributive Property to multiply this out:
8sin%28theta%29cos%5E3%28theta%29-4sin%28theta%29cos%28theta%29
which happens to be the expression we want!