Question 607036: Can someone graciously help me on this problem, please?
Solve sin(6x)cos(9x)+cos(6x)(9x)= -0.55 for the smallest positive solution.
x= ?
Thank you.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I assume your equation is really:
sin(6x)cos(9x)+cos(6x)sin(9x)= -0.55. If not then the rest of this will not solve your problem. (But it may teach you something nevertheless!)
Solving equations like yours often involves the following three steps:- Transform the equation, using algebra and/or Trig properties/formulas, into one or more equations of the form:
TrigFunction(expression) = number - Because of the periodicity of Trig functions there will be an infinite number of solutions to the equation(s) found in step 1. Express these infinite solutions in a general solution. (You'll see how shortly.)
- Sometimes the problem asks for specific solutions, like "smallest positive", or for solutions within a specific interval. (If not, then your problem is already finished!) Use the general solution to determine the specific solution(s). (Again, you'll see how shortly.
Let's see this in action.
1) Transform the equation into the desired form.
It can help a lot if you are able to look upon your Trig formulas as patterns. Your problem is a perfect example. The left side of your equation:
sin(6x)cos(9x)+cos(6x)sin(9x)= -0.55
exactly matches the pattern in the sin(A+B) formula:
sin(A+B) = sin(A)cos(B) + cos(A)sin(B)
with the "A" being 6x and the "B" being 8x. So according to this pattern, your left side is equal to:
sin(6x+9x) = -0.55
which simplifies to:
sin(15x) = -0.55
We now have the equation in the desired form.
2) Find the general solution. This involves doing the following for each of the equations from step 1:- Using the "number" portion of the equation and your knowledge of special angles or a calculator, find the reference angle. Ignore the sign of the "number" when finding a reference angle.
- Use the sign of the "number" and the particular Trig function to determine the quadrants in which the angles terminate.
- Write equations of the following form:
"exspression" = angle-in-proper-quad.-with-proper-ref.-angle +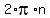 
where "expression" is whatever the argument is to the Trig function.
Let's see this in action: 1) Find the reference angle. Since 0.55 is not a special angle value, we need to use a calculator. My calculator gives  , (Feel free to round off this number as desired.) 2) Determine quadrants. the sin function is negative in the 3rd and 4th quadrants. 3) Write the equations and solve for the variable:
 (where "n" can be any integer)
 (where "n" can be any integer)
The "15x" comes from sin(15x). The first equation is for the solutions that terminate in the 3rd quadrant and the second equation is for the solutions that terminate in the 4th quadrant.
Now we solve for x. Dividing both sides by 15 we get:
 (where "n" can be any integer)
 (where "n" can be any integer)
These equations are the general solution.
3. Find the specific solution, if requested. To find specific solutions you try various integer values for the "n" in your general solution equations. Be sure to use all the equations in the general solution and to try enough values for "n" so that you can be sure you have the right specific solution(S). Your problem asks for the smallest positive solution. First let's replace the  's with 3.1415927 in both equations:
 (where "n" can be any integer)
and simplify:
 (where "n" can be any integer)
 (where "n" can be any integer)
Now we can start trying various integers for "n". You should find that the smallest positive x comes when n = 0 in the first equation:
|
|
|
