SOLUTION: solve for x using trigonometry for the interval [0, 2π) sin^2x= 1/2 The x after the 2 is NOT a part of the exponent.

Algebra ->  Algebra  -> Trigonometry-basics -> SOLUTION: solve for x using trigonometry for the interval [0, 2π) sin^2x= 1/2 The x after the 2 is NOT a part of the exponent.       Log On

Ad: Algebra Solved!™: algebra software solves algebra homework problems with step-by-step help!
Ad: Algebrator™ solves your algebra problems and provides step-by-step explanations!

   

Question 582240: solve for x using trigonometry for the interval [0, 2π)
sin^2x= 1/2
The x after the 2 is NOT a part of the exponent.
Answer by KMST(1869) About Me  (Show Source):
You can put this solution on YOUR website!
%28sin%28x%29%29%5E2=1%2F2
There is a positive and a negative value for sin%28x%29.
The positive solution is:
The negative solution is: sin%28x%29=-sqrt%281%2F2%29=-sqrt%282%29%2F2=sin%285pi%2F4%29=sin%287pi%2F4%29
Those four angles pi%2F4, 3pi%2F4, 5pi%2F4 and 7pi%2F4 are the solution.
The reference angle is 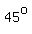pi%2F4, or 45%5Eo for those allergic to pi.
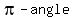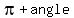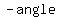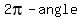For each (first quadrant) reference angle there is, in each of the other quadrants, a "reflection" angle that has the same absolute value for all trigonometric functions. It is pi-angle, the reflection on the y axis, for the second quadrant. It is pi%2Bangle, the reflection on the origin, for the third quadrant, and -angle, or 2pi-angle if you want it positive, the reflection on the x axis, for the third quadrant.